1、填空题  有一质点在连续12秒内做匀加速直线运动，在第一个4秒内位移为24m，在最后4秒内位移为56m，则质点的加速度大小为______m/s2．

参考答案：设相等时间为T，T=4s，根据匀变速直线运动在连续相等时间内的位移之差是一恒量，得，
x3-x1=2aT2
解得a=x3-x12T2=56-242×16m/s2=1m/s2．
故答案为：1m/s2．

本题解析：

本题难度：一般

2、选择题  有一系列斜面，倾角各不相同，它们的底端相同，都是O点，如图所示。有一系列完全相同的滑块（可视为质点）从这些斜面上的A、B、C、D……各点同时由静止释放，下列判断正确的是?（?）
A．若各斜面均光滑，且这些滑块到达0点的速率相同，则A、B、C、D……各点处在同一水平线上
B．若各斜面均光滑，且这些滑块到达O点的速率相同，则A、B、C、D……各点处在同一竖直面内的圆周上
C．若各斜面均光滑，且这些滑块到达O点的时间相同，则A、B、C、D……各点处在同一水平线上
D．若各斜面均光滑，且这些滑块到达O点的时间相同，则A、B、C、D……各点处在同一竖直面内的圆周上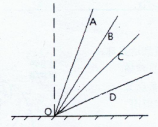

参考答案：AD

本题解析：若各斜面均光滑，且这些滑块下滑时的加速度由重力沿斜面向下的分力产生的
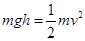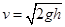A、这种情况下机械能守恒，由可得，，所以若这些滑块到达0点的速率相同，则A、B、C、D……各点处在同一水平线上.所以A对
B、原因同上，所以B错
C、设斜面倾角为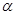，A、B、C、D……各点处在同一水平线上则h相同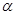，不同，沿斜面下滑的距离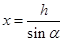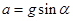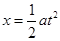，，，可得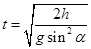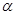，不同，则t不同，所以C错.
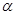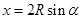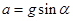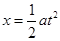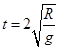D、若A、B、C、D……各点处在同一竖直面内的圆周上，设斜面倾角为，圆周半径为R，则，，，可得，与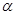无关，所以D对。
故选AD.
点评：本题难点在于在A、B、C、D……各点处在同一竖直面内的圆周上向下滑的时间的计算，一定要找到一个不变的量—R，把个斜面联系起来。

本题难度：简单

3、简答题  如图，在倾角为θ的光滑斜面上，有两个用轻质弹簧相连接的物体A、B．它们的质量分别是mA和mB，弹簧的劲度系数k，C为一固定挡板．系统处于静止状态．现开始用一恒力F沿斜面方向拉物体A，使之沿斜面向上运动．若重力加速度为g，求：
（1）物体B刚离开C时，物体A的加速度a．
（2）从开始到物体B刚要离开C时，物体A的位移d．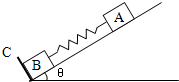

参考答案：（1）系统静止时，弹簧处于压缩状态，分析A物体受力可知：
F1=mAgsinθ，F1为此时弹簧弹力，设此时弹簧压缩量为x1，
则F1=kx1，得x1=mAgsinθk
在恒力作用下，A向上加速运动，弹簧由压缩状态逐渐变为伸长状态．当B刚要离开C时，弹簧的伸长量设为x2，分析B的受力有：
kx2=mBgsinθ，
得x2=mBgsinθk
设此时A的加速度为a，由牛顿第二定律有：
F-mAgsinθ-kx2=mAa，
得a=F-(mA+mB)gsinθmA
（2）A与弹簧是连在一起的，弹簧长度的改变量即A上移的位移，故有d=x1+x2，
即有：d=(mA+mB)gsinθk
答：（1）物体B刚离开C时，物体A的加速度a=F-(mA+mB)gsinθmA；
（2）从开始到物体B刚要离开C时，物体A的位移d=(mA+mB)gsinθk．

本题解析：

本题难度：一般

4、选择题  做匀加速直线运动的物体，运动了t秒，则（　　）
A．它的加速度越大，通过的路程一定越长
B．它的初速度越大，通过的路程一定越长
C．物体的末速度越大，通过的路程一定越长
D．物体的平均速度越大，通过的路程一定越长

参考答案：A、由S=V0t+12at2可知，t是确定的，当加速度a较大时，x的大小不确定的（因V0不知），所以A错误
B、由S=V0t+12at2可知，t是确定的，当初速度V0较大时，x的大小不确定的（因a不知），所以B错误；
C、利用逆过程分析，S=V末t-12at2可知，t是确定的，当末速度V末较大时，x的大小不确定（因a不知），所以C错误；
D、根据物体的平均速度公式.v=xt可知，由x=V平t，所以物体的平均速度越大，通过的路程一定越长，所以D正确．
故选D．

本题解析：

本题难度：一般

5、简答题  如图所示为仓库中常用的皮带传输装置示意图，它由两台皮带传送机组成，一台水平，A、B两端相距3m，另一台倾斜，传送带与地面的倾角θ=37°，C、D相距4.45m，B、C相距很近．水平部分AB以?v0=5m/s的速率顺时针匀速转动．将质量为10kg的一袋大米无初速度地放在A端，到达B端后，速度大小不变地传到倾斜的CD部分，米袋与传送带间的动摩擦因数均为0.5，g=10m/s2，sin37°=0.6，cos37°=0.8．
（1）若CD部分传送带不运转，求米袋沿传送带所能上升的最大距离．
（2）若要米袋能被传送到D端，求CD部分顺时针运转的最小速度，以及米袋从C端到?D端所用的最长时间．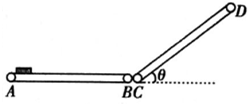

参考答案：（1）米袋在AB上加速时的加速度a0=μmgm=μg=5m/s2．
米袋的速度达到v0=5m/s时，滑行的距离s0=v022a0=2.5m＜AB=3m，因此米袋在到达B点之前就与传送带达到共速．
设米袋在CD上运动的加速度大小为a，由牛顿第二定律得，
mgsinθ+μmgcosθ=ma
代入数据得a=10m/s2．
所以米袋沿传送带所能上升的最大距离s=v022a=1.25m．
（2）设CD部分运转速度为v时米袋恰能到达D点（即米袋到达D点时速度恰好为零），则米袋速度减为v之前的加速度为a1=gsinθ+μgcosθ=10m/s2．
米袋速度小于v至减为零前的加速度大小为a2=gsinθ-μgcosθ=2m/s2．
由v02-v22a1+v22a2=4.45m．
解得v=4m/s，即要把米袋送到D点，CD部分顺时针运转的最小速度为4m/s．
米袋恰能运到D点所用时间最长为tm=v0-va1+va2=2.1s．
答：（1）米袋沿传送带所能上升的最大距离为1.25m．
（2）CD部分顺时针运转的最小速度为4m/s，米袋从C端到 D端所用的最长时间为2.1s．

本题解析：

本题难度：一般