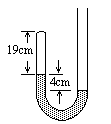
1、简答题  如图所示，竖直放置的U型管，左端封闭，右端开口，管内水银将长19cm的空气封在左管内，此时两管内水银面的高度差为4cm，大气压为标准大气压．要使两管内水银面高度差为2cm，则需注入水银柱长度为多少．

参考答案：
3cm或9cm

本题解析：

本题难度：简单

2、计算题  若一条鱼儿正在水下10m处戏水，吐出的一个体积为1cm3的气泡．气泡内的气体视为理想气体，且气体质量保持不变，大气压强为P0=1.0×105Pa，g=10m/s2，湖水温度保持不变．
①气泡在上升的过程中，气体吸热还是放热？请简述理由。
②气泡到达湖面时的体积多大？

参考答案：① 吸热 ②2cm3

本题解析：① 吸热（1分），气泡上升的过程中体积增大，对外做功，由于保持温度不变，故内能不变，由热力学第一定律可得，气泡需要吸热（2分）。
②气泡初始时的压强P1= P0+ρgh=2.0×105Pa              (2分)
气泡浮到水面上的气压P1= P0=1.0×105Pa
由气体的等温变化可知，P1V1= P2V2         (2分)
带入数据可得：V2=2cm3         (1分)
考点：热力学第一定律，气体实验定律

本题难度：一般

3、选择题  下列各图中，P表示压强，V表示体积，T表示热力学温度，T表示摄氏温度，各图中正确描述一定质量理想气体等压变化规律的是
[? ]
A.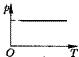
B.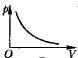
C.
D.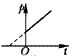

参考答案：AC

本题解析：

本题难度：一般

4、计算题  如图所示，一根粗细均匀、内壁光滑、竖直放置的玻璃管下端密封，上端封闭但留有一抽气孔。管内下部被活塞封住一定量的气体（可视为理想气体），气体温度为T1。开始时，将活塞上方的气体缓慢抽出，当活塞上方的压强达到P0时，活塞下方气体的体积为V1，活塞上方玻璃管的容积为2.6V1。活塞因重力而产生的压强为0.5p0，继续将活塞上方抽成真空并密封。整个抽气过程中管内气体温度始终保持不变。然后将密封的气体缓慢加热。求：
（1）活塞刚碰到玻璃管顶部时气体的温度；
（2）当气体温度达到1.8T1时气体的压强。

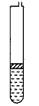
参考答案：解：（1）由玻意耳定律得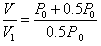：，式中V是抽成真空后活塞下方气体体积
由盖·吕萨克定律得：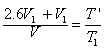
解得：T"=1.2T1
（2）由查理定律得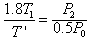
解得：p2=0.75P0

本题解析：

本题难度：一般

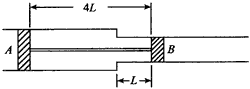
5、计算题  一个水平放置的气缸，由两个截面积不同的圆筒联接而成。活塞A、B用一长为4L的刚性细杆连接，L= 0.5 m，它们可以在筒内无摩擦地左右滑动。A、B的截面积分别为SA=40 cm2，SB=20 cm2，A、B之间封闭着一定质量的理想气体，两活塞外侧（A的左方和B的右方）是压强为P0=1.0×105Pa的大气。当气缸内气体温度为T1=525 K时两活塞静止于如图所示的位置。
（1）现使气缸内气体的温度缓慢下降，当温度降为多少时活塞A恰好移到两圆筒连接处？
（2）若在此变化过程中气体共向外放热500 J，求气体的内能变化了多少？

参考答案：解：（1）对活塞受力分析，活塞向右缓慢移动过程中，气体发生等压变化
由盖·吕萨克定律有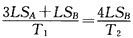
代人数值，得T2=300 K时活塞A恰好移到两筒连接处
（2）活塞向右移动过程中，外界对气体做功W=P0·3L（SA－SB）=1×105×3×0.5×（4×10-3－2×10-3）J=300 J
由热力学第一定律得△U=W+Q=300－500 J=-200 J
即气体的内能减少200 J

本题解析：

本题难度：困难