1、简答题
⑴匀强电场的场强E;
⑵AD之间的水平距离d;
⑶已知小颗粒在轨迹DP上某处的最大速度为vm,该处轨迹的
曲率半径是距水平面高度的k倍,则该处的高度为多大?
参考答案:(1) mg/q(2)
mg/q(2) (3)
(3)
本题解析:⑴小球受力如图所示?qE=mgcotα…(2分)? E= mg/q…………(2分)
mg/q…………(2分)
⑵设小球在D点速度为vD,在水平方向由牛顿第二定律得:
qE=max………………(1分)? ………………………………(2分)
………………………………(2分)
小球在D点离开水平面的条件是:?qvDB=mg……………………………(1分)
得:d= ……………………………………………………………(2分)
……………………………………………………………(2分)
 ⑶当速度方向与电场力和重力合力方向垂直
⑶当速度方向与电场力和重力合力方向垂直
时,速度最大,……………………(1分)
则: ……(2分)
……(2分)
R = kh ………………………………(1分)
 …………………(3分)
…………………(3分)
本题难度:一般
2、计算题 一质量为m、电量为q的带电质点,从y轴上y=h处的P1点以一定的水平初速度沿x轴负方向进入第二象限。然后经过x轴上x=-2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动。之后经过y轴上y=-2h处的P3点进入第四象限。已知重力加速度为g。求:
(1)粒子到达P2点时速度的大小和方向;
(2)第三象限空间中电场强度和磁感应强度的大小;
(3)带电质点在第四象限空间运动过程中最小速度的大小和方向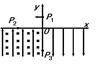
参考答案:(1) .
.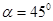 (2)
(2)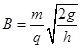 (3)
(3) ,水平向右
,水平向右
本题解析:



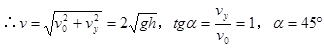

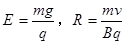
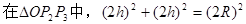


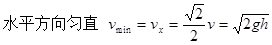 ?方向:水平向右
?方向:水平向右
点评:做此类问题时,需要先画出粒子的运动轨迹,然后结合几何知识求出粒子的半径
本题难度:一般
3、简答题 在xOy平面内,x>0的区域存在垂直纸面向里的匀强磁场,磁感应强度为B=0.4T;x<0的区域存在沿x轴正方向的匀强电场.现有一质量为m=4.0×10-9kg,带电荷量为q=2.0×10-7C的正粒子从x轴正方向上的M点以速度v0=20m/s进入磁场,如图所示,v0与x轴正方向的夹角θ=45°,M点与O点相距为l=
m.已知粒子能以沿着y轴负方向的速度垂直穿过x轴负半轴上的N点,不计粒子重力.求:(1)粒子穿过y轴正半轴的位置以及此时速度与y轴负方向的夹角;
(2)x<0区域电场的场强;
(3)试问粒子能否经过坐标原点O?若不能,请说明原因;若能,请求出粒子从M点运动到O点所经历的时间.

参考答案:(1)粒子在磁场中做匀速圆周运动时,由洛伦兹力提供向心力
Bqv0=mv20R
得:R=1m
过M点做初速度v0的垂线交y轴正方向于P点,则
PM=lcos45°
得:PM=2 m=2R
由几何关系得PM为轨迹圆的直径,P点即为粒子穿过y轴正半轴的位置
OP=PMsin45°=
本题解析:
本题难度:一般
4、填空题 如图所示,倾角为θ的光滑绝缘斜面,处在方向垂直斜面向上的匀强磁场和沿斜面方向的匀强电场中,有一质量为m、带电荷量为-q的小球,恰可在斜面上做匀速圆周运动、其角速度为ω,那么,匀强磁场的磁感应强度的大小为___________,未知电场的场强的大小为___________,方向沿___________。

参考答案:mω/q,mgsinθ/q,斜面向下
本题解析:
本题难度:一般
5、计算题 如图在xoy坐标内,在0≤x≤6m的区域存在以ON为界的匀强磁场B1、B2,磁场方向均垂直xoy平面,方向如图,大小均为1T。在x>6m的区域内存在沿y轴负方向的匀强电场,场强大小为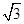 ×104V/m。一带正电的粒子(不计重力),其比荷q/m=1.0×104C/kg,从A板静止出发,经过加速电压(电压可调)加速后从坐标原点O沿x轴正方向射入磁场B1。
×104V/m。一带正电的粒子(不计重力),其比荷q/m=1.0×104C/kg,从A板静止出发,经过加速电压(电压可调)加速后从坐标原点O沿x轴正方向射入磁场B1。

(1)要使该带电粒子经过坐标为(3,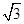 )的P点(P点在ON线上),求最大的加速电压U0;
)的P点(P点在ON线上),求最大的加速电压U0;
(2)满足第(1)问加速电压的条件下,粒子再次通过x轴时到坐标原点O的距离和速度大小;
(3)粒子从经过O点开始计时,到达P点的时间。
参考答案:(1)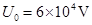 ;
;
(2) M点到O点的距离为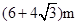 ,通过x轴的速度为
,通过x轴的速度为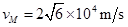 ;(3)
;(3)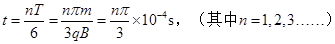
本题解析:(1)加速电压最大时,速度最大,粒子进入磁场过P点的轨迹圆弧半径最大,如图1所示:

由几何知识(圆弧的弦切角等于所对应的圆心角的一半)可知:
粒子在磁场中的轨道半径为 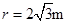
洛伦兹力提供向心力?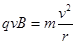
根据动能定理,电场加速过程有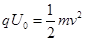 ?
?
解得 ,
,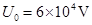
(2)P为ON中点,由轨迹的对称性可知,粒子运动轨迹如图1所示,粒子经过N点,其坐标为(6, 2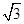 ),并且以平行于x轴的速度射入电场区域,设再次到达x轴的位置为M点,N到M过程中:
),并且以平行于x轴的速度射入电场区域,设再次到达x轴的位置为M点,N到M过程中:
x轴方向: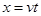
y轴方向: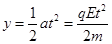
由动能定理?
联立解得: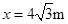 ,M点到O点的距离为
,M点到O点的距离为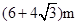
粒子在M点的速度为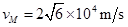
(3)带电粒子在磁场中做匀速圆周运动的周期为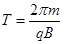 ,与粒子的运动速度无关
,与粒子的运动速度无关
粒子通过P点的轨迹还可能如图2所示:
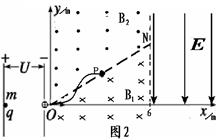
每一段圆弧对应的圆心角都是60°,对应的运动时间都是T/6,考虑到运动的重复性,可知
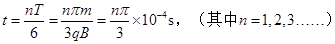
(如果只求出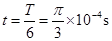 ,本小题给1分)
,本小题给1分)
本题难度:一般