1、计算题  (14分)在拆装某种大型电磁设备的过程中，需将设备内部的处于强磁场中的线圈先闭合，然后再提升直至离开磁场，操作时通过手摇轮轴A和定滑轮O来提升线圈．假设
该线圈可简化为水平长为L、上下宽度为d的矩形线圈，其匝数为n，总质量为M，总电阻为R.磁场的磁感应强度为B，如图13所示．开始时线圈的上边缘与有界磁场的上边缘平齐，若转动手摇轮轴A，在时间t内把线圈从图示位置匀速向上拉出磁场．求此过程中：
(1)流过线圈中每匝导线横截面的电荷量是多少 ?
(2)在转动轮轴时，人至少需做多少功？(不考虑摩擦影响)

参考答案：(1)　(2)Mgd＋

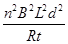
本题解析：(1)在匀速提升的过程中线圈运动速度v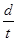＝?①
线圈中感应电动势E＝nBLv? ②
产生的感应电流I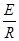＝?③
流过导线横截面的电荷量q＝It?④
联立①②③④得q＝.
(2)匀速提升的过程中，要克服重力和安培力做功，即
W＝WG＋W安?⑤
又WG＝Mgd? ⑥
W安＝nBILd⑦
联立①②③④⑤⑥⑦得
W＝Mgd＋.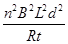

本题难度：一般

2、计算题  如图4－4－22所示，一水平放置的平行导体框宽度L＝0.5 m，接有R＝0.2 Ω的电阻，磁感应强度B＝0.4 T的匀强磁场垂直导轨平面方向向下，现有一导体棒ab跨放在框架上，并能无摩擦地沿框架滑动，框架及导体棒ab电阻不计，当ab以v＝4.0 m/s的速度向右匀速滑动时，试求：

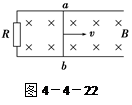
(1)导体棒ab上的感应电动势的大小及感应电流的方向；
(2)要维持ab向右匀速运动，作用在ab上的水平外力为多少？方向怎样？
(3)电阻R上产生的热功率多大？

参考答案：(1)0.8 V　由b向a　；(2)0.8 N　水平向右；(3)3.2 W

本题解析：(1)导体棒ab垂直切割磁感线，产生的电动势大小为
E＝BLv＝0.4×0.5×4.0 V＝0.8 V，
由右手定则知感应电流的方向由b向a.
(2)导体棒ab相当于电源，由闭合电路欧姆定律得
回路电流I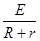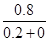＝＝?A＝4.0 A，
导体棒ab所受的安培力
F＝BIL＝0.4×0.5×4.0 N＝0.8 N，
由左手定则知其方向水平向左．
ab匀速运动，所以水平拉力F′＝F＝0.8 N，方向水平向右．
(3)R上的热功率：P＝I2R＝4.02×0.2 W＝3.2 W.

本题难度：一般

3、计算题  如图所示，电阻忽略不计的、两根平行的光滑金属导轨竖直放置，其上端接一阻值为3 Ω的定值电阻R. 在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B、磁场区域的高度为d="0.5" m. 导体棒a的质量ma="0.2" kg,电阻Ra="3" Ω；导体棒b的质量mb="0.l" kg，电阻Rb="6" Ω.它们分别从图中M、N处同时由静止开始在导轨上无摩擦向下滑动，且都能匀速穿过磁场区域，当b刚穿出磁场时a正好进入磁场. 设重力加速度为g="l0" m/s2. （不计a、b之间的作用，整个运动过程中a、b棒始终与金属导轨接触良好）求：

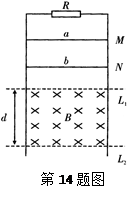
（1）在整个过程中，a、b两棒克服安培力分别做的功；
（2）a进入磁场的速度与b进入磁场的速度之比；
（3）分别求出M点和N点距L1的高度.

参考答案：（1）0.5J；（2）3：4；（3）0.75 m

本题解析：（16分）考查电磁感应与能量问题、电路问题和力学问题的综合应用．
解析(1)因a、b在磁场中匀速运动，由能量关系知
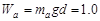?J?（2分）
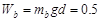J?（2分）
（2）b在磁场中匀速运动时：速度为vb，总电阻R1="7.5" Ω?（1分）
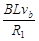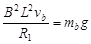b中的电流Ib=?（1分）
?（1分）
同理，a棒在磁场中匀速运动时：速度为va，总电阻R2="5" Ω?（1分）
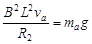?（1分）
由以上各式得: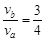?（1分）
（3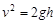）?（1分）
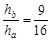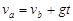?（1分）
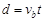?（1分）
?（1分）
由以上各式得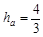?m="1.33" m?（1分）
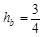?m="0.75" m?（1分）

本题难度：一般

4、计算题  （15分）如图所示，在平面的第一象限和第二象限区域内，分别存在场强大小均为E的匀强电场Ⅰ和Ⅱ，电场Ⅰ的方向沿x轴正方向，电场Ⅱ的方向沿y轴的正方向。在第三象限内存在着垂直于平面的匀强磁场Ⅲ，Q点的坐标为（－x0，0）。已知电子的电量为－e，质量为m（不计电子所受重力）。

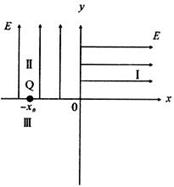
（1）在第一象限内适当位置由静止释放电子，电子经匀强电场Ⅰ和Ⅱ后恰能透过Q点。求释放点的位置坐标x、y应满足的关系式；
（2）若要电子经匀强电场Ⅰ和Ⅱ后过Q点时动能最小，电子应从第一象限内的哪点由静止释放?求该点的位置和过Q点时的最小动能。
（3）在满足条件（2）的情况下，若想使电子经过Q后再次到达y轴时离坐标原点的距离为x0，求第三象限内的匀强磁场的磁感应强度B的大小和方向。

参考答案：（1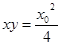）（2）电子从第一象限内的P(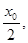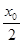)点由静止释放过Q点时动能最小，过Q点时的最小动能是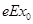（3）

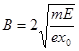
本题解析：(1)设电子从第一象限内坐标为(x，y)处由静止释放能过Q点，到达y轴时的速度为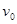，由动能定理得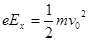：①?(1分)
若能到达Q点，则应满足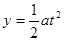：②? (1分)
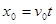③? (1分)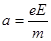④? (1分)
联立①②③④得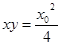：⑤? (1分)
(2)由动能定理得：电子从P点由静止释放，经匀强电场I和Ⅱ后过Q点时动能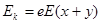：⑥? (1分)而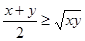?(当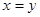时取“=”)⑦? (1分)
由⑤⑥⑦得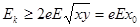：(当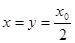时取“=”)⑧? (1分)
所以电子从第一象限内的P(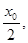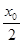)点由静止释放过Q点时动能最小，过Q点时的最小动能是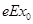
(3)若匀强磁场Ⅲ方向垂直纸面向里，则电子左偏，不会再到达y轴，所以匀强磁场方向垂直纸面向外．运动轨迹如图，则：
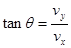而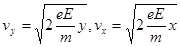
在满足条件(2)的情况下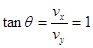所以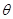=45°⑨? (1分)
设在匀强磁场Ⅲ中做匀速圆周运动的半径为r，到达y轴上的A点，结合题中条件可推知，电子在磁场中运动的轨迹应为以QA为直径的半圆，OA=x0，由几何知识知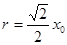：⑩? (1分)
设到达Q点的速度为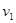，则? (1分)
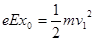
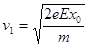
解得：? (1分)
根据牛顿第二定律得：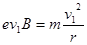
解得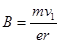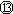：? (1分)
把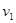和r的值代入，第三象限内的匀强磁场的磁感应强度
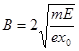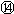?? (2分)

本题难度：一般

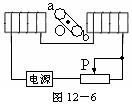
5、选择题  如图12－6所示，ab是一个可绕垂直于纸面的轴O转动的闭合矩形导线框．当滑动变阻器的滑片P自左向右滑动时，从纸外向纸内看，线框ab将（?）

A．保持静止不动
B．逆时针转动
C．顺时针转动
D．发生转动，但电源极性不明，无法确定转动方向．

参考答案：C

本题解析：无论电源的极性如何，在两电磁铁中间的区域内应产生水平的某一方向的磁场，当滑片P向右滑动时，电流减小，两电磁铁之间的磁场减弱，即穿过ab线圈的磁通量减小．虽然不知ab中感应电流的方向，但由楞次定律中的“阻碍”可直接判定线框ab应顺时针方向转动（即向穿过线框的磁通量增加的位置――竖直位置转动）．

本题难度：一般