1、计算题  【选修3-5选做题】
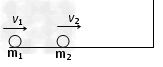
质量分别为m1和m2的两个小球在光滑的水平面上分别以速度v1、v2同向运动并发生对心碰撞，碰后m2被右侧的墙原速弹回，又与m1相碰，碰后两球都静止，求：第一次碰后m1球的速度。

参考答案：解：根据动量守恒定律得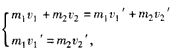
解得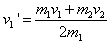

本题解析：

本题难度：一般

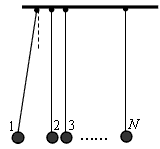
2、计算题  某兴趣小组设计了一种实验装置，用来研究碰撞问题，其模型如图所示。用完全相同的轻绳将N个大小相同、质量不等的小球并列悬挂于一水平杆、球间有微小间隔，从左到右，球的编号依次为1、2、3……N，球的质量依次递减，每球质量与其相邻左球质量之比为k（k＜1）。将1号球向左拉起，然后由静止释放，使其与2号球碰撞，2号球再与3号球碰撞……所有碰撞皆为无机械能损失的正碰。（不计空气阻力，忽略绳的伸长，g取10 m/s2）
（1）设与n＋1号球碰撞前，n号球的速度为vn，求n＋1号球碰撞后的速度。
（2）若N＝5，在1号球向左拉高h的情况下，要使5号球碰撞后升高16h（16 h小于绳长），问k值为多少？

参考答案：解：（1）设n号球质量为m，n＋1号球质量为mn＋1，碰撞后的速度分别为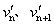，取水平向右为正方向，据题意有n号球与n＋1号球碰撞前的速度分别为vn、0
根据动量守恒有：mnvn=mnvn′+kmnvn+1′
根据机械能守恒有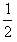：mnvn2=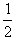mnvn′2+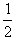kmnvn+1′2
解得：vn+1′=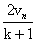(vn+1′=0舍去)
（2）设1号球摆至最低点时的速度为v1，由机械能守恒定律有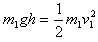
v1＝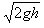
同理可求，5号球碰后瞬间的速度v5=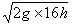
设n＋1号球与n＋2号球碰前的速度为vn＋1
据题意有：vn+1＝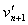
得：vn+1=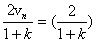nv1
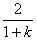n＝5时：v5＝（）4v1
解得：k＝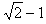

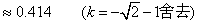
本题解析：

本题难度：困难

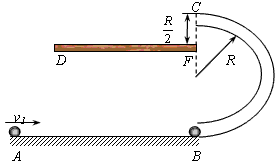
3、计算题  如图所示，一质量m1=0.2kg的小球，从光滑水平轨道上的一端A处，以v1=2.5m/s的速度水平向右运动。轨道的另一端B处固定放置一竖直光滑半圆环轨道（圆环半径比细管的内径大得多），轨道的半径R=10cm，圆环轨道的最低点与水平轨道相切；空中有一固定长为15cm的木板DF，F端在轨道最高点C的正下方，竖直距离为5cm。水平轨道的另一端B处有一质量m2=0.2kg的小球，m1、m2两小球在B处发生的是完全弹性碰撞，重力加速度为g=10m/s2。求：
（1）经过C点时，小球m2对轨道的作用力的大小及方向？
（2）m2小球打到木板DF上的位置？

参考答案：解：（1）在B处m1与m2发生的是完全弹性碰撞，有：
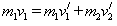?①
?②
由①②式解得：，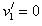
（或因m1与m2发生的是完全弹性碰撞，且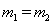，所以两球交换速度。得）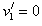
由B到C的过程，机械能守恒，有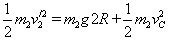 ③
由③代入数据得
在C点，对m2根据牛顿第二定律： ④
由④代入数据得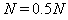：，方向竖直向下
据牛顿第三定律知：小球对轨道的作用力大小为0.5N，方向竖直向上
（2）小球从C飞出做平抛运动，有
?⑤
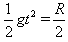?⑥
由⑤⑥解得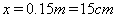：，所以物体刚好落在木板的D点上

本题解析：

本题难度：困难

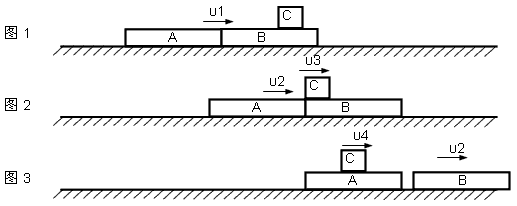
4、计算题  如图所示，A、B、C三个物体质量均为m，其中厚度相同的A、B位于光滑的水平面上，可视为质点的小物块C放在静止的B物体上，物体A以速度v0。向物体B运动，与B发生碰撞（碰撞时间极短），碰后A、B以相同的速度运动，但互不粘连；C滑过B后又在A上滑行，最后停在A上，与A一起以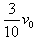的速度运动。求：
（1）物体B最终的速度；
（2）小物块C在物体A和物体B上滑行过程中由于摩擦产生的热量之比。

参考答案来源:91考试网 91ExaM.org：解：（1）从最初A以速度υ0运动到最终AC以共同速度υ4运动、同时B以速度υ2匀速运动的过程中，对ABC组成的系统全过程由动量守恒定律有：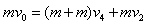
求得：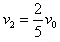
（2）如图1，从A以速度υ0运动到与B相碰获得共同速度（设为υ1）的过程中，对AB组成的系统由动量守恒定律得：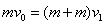
设C离开B的瞬时速度为υ3，AB整体的速度减小为υ2，如图2所示，对ABC组成的系统由动量守恒定律得：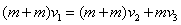
设该过程中C在B上滑行由于摩擦产生的热量为QB，由能量关系可得：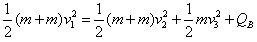
C以速度υ3离开B滑上A后，AB分离，B以速度υ2匀速运动，C和A相互作用至达到共同速度υ4，如图3所示。该过程中对A、C组成的系统由动量守恒定律有：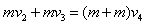
设该过程中C在A上滑行由于摩擦产生的热量为QA，由功能关系可得：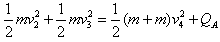
联立以上各式及题中已知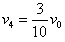，可得：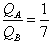

本题解析：

本题难度：困难

5、选择题  A、B两球在光滑水平面上作相向运动，已知mA＞mB，当两球相碰后，其中一球静止，则可以断定

[? ]

参考答案：C

本题解析：

本题难度：一般