1、简答题  设质子的半径为r0，氢气的摩尔质量为μ，阿伏加德罗常数为NA，万有引力恒量为G，如果在宇宙间有一个恒星的密度等于质子的密度，假想该恒星的第一宇宙速度达到光速c，电子质量忽略不计，π值取3
求：（1）该恒星的半径R；（2）该恒星表面的重力加速度g．

参考答案：设恒星的质量为m1，绕恒星运行的卫星质量为m2，则Gm1m2R2=m2c2R；
密度ρ=M2NA?43πr20=m143πR3；?
星球表面重力等于万有引力：Gm1m2R2=m2g；
由以上各式解得：R=r0c

本题解析：

本题难度：一般

2、简答题  如图所示，一个质量为m、电荷量为q的正离子，在D处沿图示方向以一定的速度射入磁感应强度为B的匀强磁场中，此磁场方向是垂直纸面向里．结果离子正好从距A点为d的小孔C沿垂直于电场方向进入匀强电场，此电场方向与AC平行且向上，最后离子打在G处，而G处距A点2d（AG⊥AC）．不计离子重力，离子运动轨迹在纸面内．求：
（1）此离子在磁场中做圆周运动的半径r；
（2）离子从D处运动到G处所需时间为多少；
（3）离子到达G处时的动能为多少．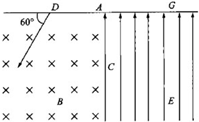

参考答案：

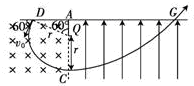
（1）正离子的运动轨迹如图所示，离子圆周运动半径r满足：
? r+rcos 60°=d　
解得：r=23d　
（2）设离子在磁场中运动的速度为v0，则有
? qv0B=mv20r
得，r=mv0qB
离子在磁场中运动的周期为? T=2πrv0=2πmqB
根据轨迹得：离子在磁场中做圆周运动的时间为：

? t1=120°360°T=2πm3qB，
离子从C运动到G做类平抛运动，水平方向做匀速直线运动，所需的时间t2=2dv0
由r=23d=mv0qB得，t2=2dv0=3mqB
故离子从D→C→G的总时间为：
? t=t1+t2=(9+2π)m3qB．　
（2）设电场强度为E，对离子在电场中的运动过程，有：
? qE=ma，d=12at22　
由动能定理得：Eq?d=EkG-12mv02　
解得：EkG=4B2q2d29m．
答：
（1）此离子在磁场中做圆周运动的半径r为23d；
（2）离子从D处运动到G处所需时间为(9+2π)m3qB；
（3）离子到达G处时的动能为4B2q2d29m．

本题解析：

本题难度：一般

3、计算题  运用纳米技术能够制造出超微电机，英国一家超微研究所宣称其制造的超微电机转子的直径只有30μm ，转速高达2000 r/min ，试估算位于转子边缘的一个质量为10 ×10-26 kg 的原子向心加速度．（保留两位有效数字）

参考答案：1. 3 m/s2

本题解析：

本题难度：一般

4、选择题  如图所示，A、B、C三物体放在旋转水平圆台上，它们与圆台间的动摩擦因数均相同，已知A的质量为m，B和C的质量均为2m，A、B离轴距离为R，C离轴距离为2R．当圆台转动时，三物均没有打滑，则：（设最大静摩擦力等于滑动摩擦力）（　　）
A．这时C的向心力最大
B．这时A物体受的摩擦力最小
C．若逐步增大圆台转速，C比B先滑动
D．若逐步增大圆台转速，B比A先滑动