1、选择题  如图所示，物体A、B用细绳与弹簧连接后跨过滑轮，A静止在倾角为45°的粗糙斜面上，B悬挂着。已知mA＝3mB，不计滑轮摩擦，现将斜面倾角由45°减小到30°．那么下列说法中正确的是(? )

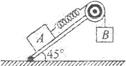
A．弹簧的弹力不变
B．物体A对斜面的压力将减小
C．物体A受到的静摩擦力将减小
D．弹簧的弹力及A受到的静摩擦力都不变

参考答案：AC

本题解析：对B受重力mBg和细绳的拉力T1作用，由于初始时A、B处于静止状态，因此有：T1＝mBg，对A受重力mAg、斜面的支持力N、摩擦力f和弹簧的拉力T2作用，不妨假设的方向沿斜面向上，有：T2＋f－mAgsin45°＝0，N－mAgcos45°＝0，对弹簧，不计质量，始终有：T1＝T2，解得：f＝－mBg，N＝，又因为mA＝3mB，所以f＞0，即其方向与假设的方向相同，当斜面倾角由45°减小到30°时，假设A、B仍然处于静止状态，同理解得：N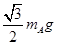＝＞，－mBg＞f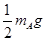＝－mBg＞0，所以假设正确，故选项A、C正确；选项B、D错误。

本题难度：一般

2、选择题  物体受三个共点力F1、F2、F3的共同作用，这三个力的合力可能为零的是
[? ]
A.F1=5N，F2=10N，F3=14N
B.F1=11N，F2=25N，F3=40N
C.F1=7N，F2=31N，F3=35N
D.F1=100N，F2=75N，F3=24N

参考答案：AC

本题解析：

本题难度：简单

3、简答题  如图12所示粗细均匀的木棒长为L，质量为M ，可绕固定转动轴O自由转动，现用水平力F作用于木棒的下端将木棒从竖直位置缓慢拉起，并转过θ角度，则在拉起的过程中，拉力F做的功为多少？

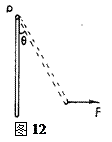
某同学解法为：
木棒与竖直位置成θ时，木棒所受的力矩平衡? Mg Lsinθ/2=" F" Lcosθ，
得到F=Mgtgθ/2
从竖直位置缓慢拉起的过程中，?拉力F从0变化到Mgtgθ/2，
拉力F的平均值=Mgtgθ/4?
拉力作用点在力F方向上的位移是? S="L" sinθ
根据W="FS?" 解得 ：拉力F 做的功：WF=" Mg" L sinθtgθ/4
所以在拉起的过程中，拉力F做的功为WF="Mg" L sinθtgθ/4 ，
你认为他的解法是否正确？若正确，请说明理由；若错误，也请说明理由，并且解出正确的结果。

参考答案：不正确
沿水平方向F力不是均匀地增加，所以不能用力的算术平均值来计算此力所做的功。
正确解法：　根据能量守恒，力F所做的功等于木棒势能增加量?
??

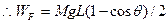
本题解析：不正确
沿水平方向F力不是均匀地增加，所以不能用力的算术平均值来计算此力所做的功。
正确解法：　根据能量守恒，力F所做的功等于木棒势能增加量?
??

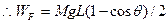
本题难度：一般

4、计算题  （8分）如图8所示，一弧形的石拱桥由四块形状规则的相同的石块垒成，每块石块的左、右两个截面间所夹的圆心角为30°，第l、4块石块固定在地面上，直线OA沿竖直方向。求第2、3块石块间的作用力F23和第l、2块石块的作用力F12之比。（不计石块间的摩擦力）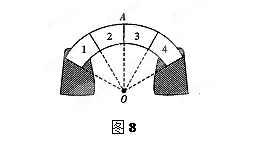

参考答案：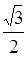
每个表达式3分，共6分。

本题解析：设每块石块的重力为G，第2、3块石块间的作用力为F23，第1、2块石块间的作用力为F12，以第二块石块为研究对象，进行受力分析。?
由物体的平衡F12cos30°=F23，解得F23∶F12=cos30°=?。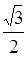
每个表达式3分，共6分。
本题考查受力平衡的问题，以第二块石块为研究对象，分析受力情况，根据力的合成或分解可知两力的关系

本题难度：一般

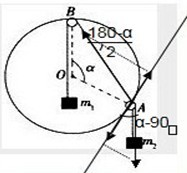
5、选择题  如图所示，小圆环A系着一个质量为m2的物块并套在另一个竖直放置的大圆环上，有一细线一端拴在小圆环A上，另一端跨过固定在大圆环最高点B的一个小滑轮后吊着一个质量为m1的物块．如果小圆环、滑轮、绳子的大小和质量以及相互之间的摩擦都可以忽略不计，绳子又不可伸长，若平衡时弦AB所对应的圆心角为α，则两物块的质量比m1：m2应为（　　）
A．cos

参考答案：如图

对小环进行受力分析，如图所示，小环受上面绳子的拉力m1g，下面绳子的拉力m2g，以及圆环对它沿着OA向外的支持力，将两个绳子的拉力进行正交分解，它们在切线方向的分力应该相等：
m1g sin180-α2=m2gcos（α-90）
即：m1cosα2=m2sinα
m1cosα2=2m2sinα2cosα2
得：m1：m2=2sinα2
故选：C．

本题解析：

本题难度：简单