1、选择题 下表是火星和地球部分数据对照表,把火星和地球视为匀质理想球体,它们绕太阳的运动近似看作匀速圆周运动,从表中数据可以分析得出
| 质量
(kg)
| 公转周期
(d天)
| 自转周期
(h小时)
| 近似公转轨道半径(m)
| 星球半径
(m)
|
火星
| 6.421×1023
| 686.98
| 24.62
| 2.28×1011
| 3.395×106
|
地球
| 5.976×1024
| 365.26
| 23.93
| 1.50×1011
| 6.378×106
|
A.地球所受向心力较大 B.地球公转动能较大
C.火星两极处地表重力加速度较大 D.火星的第一宇宙速度较大
参考答案:AB
本题解析:A、根据F=G 得:根据图表可知,地球质量约为火星半径的10倍,公转轨道半径约为火星的0.65倍,所以地球所受向心力较大,故A正确;
得:根据图表可知,地球质量约为火星半径的10倍,公转轨道半径约为火星的0.65倍,所以地球所受向心力较大,故A正确;
B、根据G =m
=m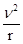 得:v=
得:v= ,地球公转轨道半径约为火星的0.65倍,所以速度约为火星速度的
,地球公转轨道半径约为火星的0.65倍,所以速度约为火星速度的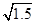 倍,动能Ek=
倍,动能Ek=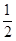 mv2,地球质量约为火星半径的10倍,所以地球公转动能约为火星的15倍,故B正确;
mv2,地球质量约为火星半径的10倍,所以地球公转动能约为火星的15倍,故B正确;
C、根据G =mg得:g=G
=mg得:g=G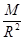 ,地球半径约为火星的2倍,地球质量约为火星半径的10倍,所以地表重力加速度约为火星的2.5倍,故C错误;
,地球半径约为火星的2倍,地球质量约为火星半径的10倍,所以地表重力加速度约为火星的2.5倍,故C错误;
D、第一宇宙速度v=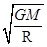 ,地球半径约为火星的2倍,地球质量约为火星半径的10倍,所以地球的第一宇宙速度是火星的
,地球半径约为火星的2倍,地球质量约为火星半径的10倍,所以地球的第一宇宙速度是火星的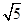 倍,,D错误.
倍,,D错误.
本题应用牛顿第二定律研究行星运动的问题,关键是要灵活选择向心力公式的形式.
本题难度:一般
2、选择题 如果把水星和金星绕太阳的运动视为匀速圆周运动,从水星与金星在一条直线上开始计时,若天文学家测得在相同时间内水星转过的角度为θ1;金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件可求得
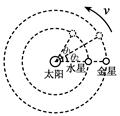
A.水星和金星绕太阳运动的周期之比
B.水星和金星的密度之比
C.水星和金星到太阳的距离之比
D.水星和金星绕太阳运动的向心加速度大小之比
参考答案:ACD
本题解析:由相同时间的角度可得角速度之比,周期与角速度成反比,A正确;由于求不出水星和金星的质量和半径,B错误;由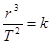 ,C正确;由
,C正确;由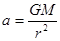 知,D正确。
知,D正确。
本题难度:困难
3、填空题 某一行星有一质量为m的卫星,以半径r,周期T做匀速圆周运动,行星的质量
参考答案: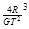
本题解析:
考点:万有引力定律及其应用.
分析:由万有引力提供向心力,可以列式求解;
解:设行星的质量为M,由行星对卫星的万有引力提供向心力得
G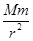 =
= r=ma
r=ma
解之得
M=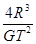
故答案为: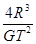
本题难度:一般
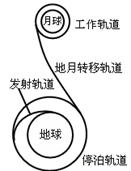
4、其他 2007年10月24日18时05分“嫦娥一号”发射升空,“嫦娥一号”探月卫星的路线简化后示意图如图所示。卫星由地面发射后经过发射轨道进入停泊轨道,然后在停泊轨道经过调速后进入地---月转移轨道,再次调速后进入工作轨道,卫星开始对月球进行探测。若地球与月球的质量之比为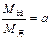 ,卫星的停泊轨道与工作轨道的半径之比为
,卫星的停泊轨道与工作轨道的半径之比为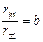 ,卫星在停泊轨道和工作轨道上均可视为做匀速圆周运动,求卫星在停泊轨道和工作轨道运行的线速度大小之比
,卫星在停泊轨道和工作轨道上均可视为做匀速圆周运动,求卫星在停泊轨道和工作轨道运行的线速度大小之比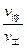 。
。
参考答案: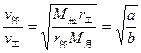
本题解析: 设“嫦娥一号”卫星质量为m,引力常量为G.
卫星在停泊轨道运行时,地球对其万有引力提供圆周运动的向心力,则
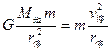 …①(2分) 所以
…①(2分) 所以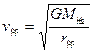 …②(1分)
…②(1分)
卫星在工作轨道运行时,月球对其万有引力提供圆周运动的向心力,则
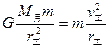 ……③(2分) 所以:
……③(2分) 所以: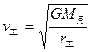 …………④(1分)
…………④(1分)
联立②④式得: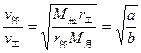 ………………………………⑤(3分)
………………………………⑤(3分)
本题难度:一般
5、填空题 两颗人造卫星A、B绕地球做匀速圆周运动,它们的周期之比TA∶TB=1∶8,则其轨道半径之比是 运动速率之比是
参考答案:1:4 2:1
本题解析:分析:人造卫星绕地球做圆周运动受到的万有引力提供向心力,分别用周期、速率来表示向心力,化简公式即可求解结果.
解答:解:人造卫星绕地球做圆周运动受到的万有引力提供向心力,对A卫星有: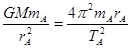 ,
,
对B卫星有: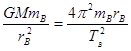 ,化简得:
,化简得: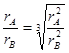 =
= 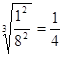 ;
;
用速度表示向心力,对A卫星有: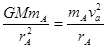 , 对B卫星有:
, 对B卫星有: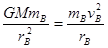 ,
,
化简得: ,
,
故答案为:1:4,2:1.
点评:对于卫星问题一定掌握:万有引力提供向心力,可以用卫星的速度、周期、角速度来分别表示向心力,从而求出结果.
本题难度:一般