1、选择题 质量为m、速度为v的A球跟质量为3m的静止B球发生正碰。碰撞可能是弹性的,也可能是非弹性的,因此,碰撞后B球的速度可能有不同的值。碰撞后B球的速度大小可能是
[? ]
A.0 6v
B.0.4v
C.0.2v
D.v
参考答案:B
本题解析:
本题难度:一般
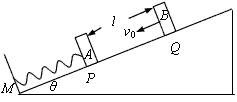
2、计算题 有一倾角为θ的斜面,其底端固定一档板,另有三个木块A、B、C,它们的质量分别为mA=mB=m,mC=3m,它们与斜面间的动摩擦因数都相同。其中木块A和一轻弹簧连接,放于斜面上,并通过轻弹簧与档板M相连,如图所示。开始时,木块A静止在P点,弹簧处于原长,木块B在Q点以初速度v0沿斜面向下运动,P、Q间的距离为l,已知木块B在下滑过程中做匀速直线运动,与木块A碰撞后立刻一起沿斜面向下运动,但不粘连,它们到达一个最低点后向上运动,木块B向上运动恰好能回到Q点。现将木块C从Q点以初速度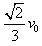 沿斜面向下运动,木块A仍静止于P点,经历同样的过程,最后木块C停在斜面上的R点(图中未画出)。求:
沿斜面向下运动,木块A仍静止于P点,经历同样的过程,最后木块C停在斜面上的R点(图中未画出)。求:
(1)A、B一起开始压缩弹簧时速度v1;
(2)A、B压缩弹簧的最大长度;
(3)P、R间的距离l"的大小。
参考答案:解:(1)木块B下滑做匀速运动,有mgsinθ=μmgcosθ
B和A碰撞后,设速度为v1,根据动量守恒定律得mv0=2mv1
解得v1=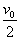
(2)设两木块向下压缩弹簧的最大长度为x,两木块被弹簧弹回到P点时的速度为v2,根据动能定理得
一μ2mgcosθ2x= 2mv
2mv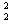 一
一 2mv
2mv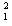
两木块在P点处分开后,木块B上滑到Q点的过程中,根据动能定理得
一(mgsinθ+μmgcosθ)l=0一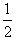 mv
mv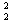
解得x=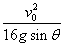 一l
一l
(3)木块C与A碰撞前后速度为v1",根据动量守恒定律得3m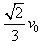 =4mv1"
=4mv1"
解得v1"=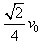
设木块C和A压缩的最大长度为x",两木块被弹簧弹回到P点时的速度为v2",根据动能定理得
一μ4mgcosθ2x"=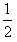 4mv"
4mv"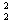 一
一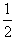 4mv"
4mv"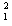
木块C与A在P点处分开后,木块C上滑到R的过程中,根据动能定理得
一(3mgsinθ+μ3mgcosθ)l"=0一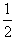 3mv"
3mv"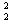
在木块压缩弹簧的过程中,重力对木块所做的功与摩擦力对木块所做的功大小相等,因此,木块B和A压缩弹簧的初动能Ek1=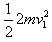 =
=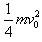
木块C与A压缩弹簧的初动能Ek2= =
=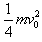
即Ek1=Ek2
因此,弹簧先后两次的最大压缩量相等,即x=x",综上可得l"=l一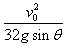
本题解析:
本题难度:困难
3、计算题 如图所示,三个可视为质点的物块A,B,C,在水平面上排成一条直线,且彼此间隔一定距离。已知mA=mB=10 kg,mC=20 kg,C的左侧水平面光滑,C的右侧水平面粗糙,A,B与粗糙水平面间的动摩擦因数μA=μB=0.4,c与粗糙水平面间动摩擦因数μC=0.2,A具有20 J的初动能向右运动,与静止的B发生碰撞后粘在一起,又与静止的C发生碰撞,最后A,B,C粘成一个整体,求:(取g=10 m/s2)
(1)在第二次碰撞中损失的机械能有多少?
(2)这个整体在粗糙的水平面上滑行的距离是多少?

参考答案:解:(1)由于A的初动能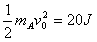
得A的初速度v0=2 m/s
A,B发生完全非弹性碰撞,根据动量守恒定律
mAv0=(mA+mB)v1,得v1=1 m/s
A,B与C发生完全非弹性碰撞,根据动量守恒定律
(mA+mB)v1=(mA+mB+mC)v2,得v2=0.5 m/s
在第二次碰撞中损失的机械能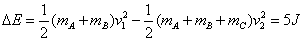
(2)A、B、C整体在粗糙水平面上所受的摩擦力f=fA+fB+fC=μAmAg+μBmBg+μCmCg=120 N
根据动能定理解得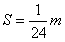
本题解析:
本题难度:困难
4、计算题 用轻弹簧相连的质量均为2 kg的A、B两物块都以v=6 m/s的速度在光滑的水平地面上运动,弹簧处于原长,质量4 kg的物块C静止在前方,如图所示,B与C碰撞后二者两者立即粘在一起运动。求:在以后的运动中:?
(1)当弹簧的弹性势能最大时,物体A的速度多大?
(2)弹性势能的最大值是多大??
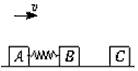
参考答案:解:(1)当A、B、C三者的速度相等时弹簧的弹性势能最大
由于A、B、C三者组成的系统动量守恒,(mA+mB)v=(mA+mB+mC)vA′ ?
解得vA′=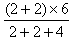 m/s=3 m/s ?
m/s=3 m/s ?
(2)B、C碰撞时B、C组成的系统动量守恒,设碰后瞬间B、C两者速度为v′,则?
mBv=(mB+mC)v′
v′=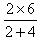 =2 m/s?
=2 m/s?
设物A速度为vA′时弹簧的弹性势能最大为Ep
根据能量守恒Ep=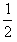 (mB+mC)
(mB+mC)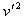 +
+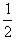 mAv2-
mAv2-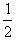 (mA+mB+mC)
(mA+mB+mC)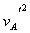 =
=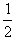 ×(2+4)×22+
×(2+4)×22+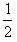 ×2×62-
×2×62-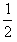 ×(2+2+4)×32=12 J
×(2+2+4)×32=12 J
本题解析:
本题难度:困难
5、简答题 如图12所示,水平平板小车质量为m=" 2kg," 其上左端放有一质量为M=6kg的铁块,铁块与平板车间的动摩擦因数μ=0.5,今二者以10m/s的速度向右运动,并与墙发生弹性碰撞,使小车以大小相同的速度反弹回,这样多次进行,求:
① 欲使M不从小车上落下,小车至少多长?
② 第一次反弹后到最终状态,小车运动的总路程.(小车与水平面的摩擦不计,g=10m/s2 )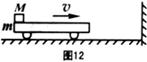
参考答案:(1) (2)
(2)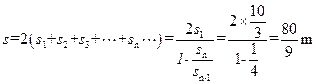
本题解析:① 取平板车与铁块为研究系统,由M>m,系统每次与墙碰后m反向时,M仍以原来速度向右运动,系统总动量向右,故会多次反复与墙碰撞,每次碰后M都要相对m向右运动,直到二者停在墙边,碰撞不损失机械能,系统的动能全在M相对m滑动时转化为内能。设M相对m滑动的距离为s,则:
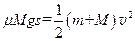 ?
?
解得: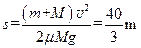 ?
?
欲便M不从小车上落下,则L≥s,故平长 ?
?
② 小车第一次反弹向左以10m/s的速度做减速运动,直到速度为零,其加速度大小为
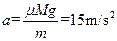 ? ( l 分)
? ( l 分)
故小车第一次向左的最大位移为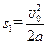 ,代入数据得
,代入数据得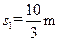 ?
?
设小车第n-1次碰前速度为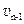 ,第n次碰前速度为
,第n次碰前速度为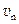 ,则第n-1次碰后到第n次碰前过程动量守恒,有:
,则第n-1次碰后到第n次碰前过程动量守恒,有: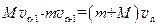 ,所以
,所以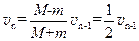 ?
?
第n-1次碰后小车反弹速度为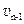 ,向左减速的最大位移为
,向左减速的最大位移为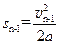 ?
?
随后向右加速距离为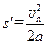 ,显然
,显然 ,所以在碰前有相等速度
,所以在碰前有相等速度
第n次碰后向左运动的最大位移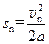 (1分),所以
(1分),所以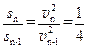 ,即成等比数列。小车运动的总路程为:
,即成等比数列。小车运动的总路程为:
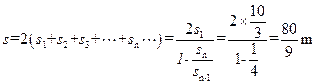
本题难度:一般