1、简答题  如图所示，电容为C、带电量为Q、极板间距为d的电容器固定在绝缘底座上，两板竖直放置，总质量为M，整个装置静止在光滑水平面上。在电容器右板上有一小孔，一质量为m、带电量为+q的弹丸以速度v0从小孔水平射入电容器中（不计弹丸重力，设电容器周围电场强度为0），弹丸最远可到达距右板为x的P点，求：
小题1:弹丸在电容器中受到的电场力的大小；
小题2:x的值；
小题3:当弹丸到达P点时，电容器电容已移动的距离s；
小题4:电容器获得的最大速度。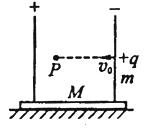

参考答案：
小题1: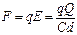
小题2: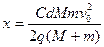
小题3: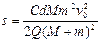
小题4: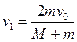

本题解析：
小题1:电容极板电压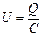?…………①
极板问场强?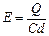?…………②?则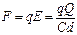?…………③
小题2:弹丸到达P点时两者有共同速度，设为v，由动量守恒有：
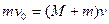?…………④
对弹丸，由动能定理得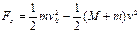：?…………⑤，
解得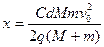?…………⑥
小题3:对电容器，由动能定理得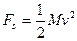：…………⑦
解得?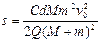?…………⑧
小题4:弹丸最终返回从右板小孔飞出，此时电容器速度最大，设电容器速度为v1、弹丸速度为v2。则由动量守恒有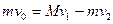：?…………⑨
在整个过程中由能量守恒，即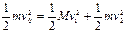?…………⑩
由⑨、⑩两式解得?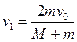?…………11

本题难度：一般

2、计算题  （10分）如图所示，水平放置的两块平行金属板长L=5cm，两板间距d=1cm，两板间电压U=91V不变，上板带正电。距离极板右端s=10cm处有一接收屏，各种速度的电子沿水平方向从两板中央射入。电子的质量=0.91×10-30kg，电荷量e=1.6×10-19C。求：

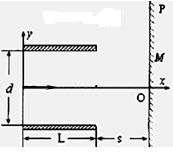
（1）到达接收屏上的电子的初速度应满足的条件；
（2）电子打到接收屏上距中心O的最大距离；

参考答案：（1）v≥2×107m/s方能打到屏上（2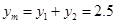）cm

本题解析：（1）电子恰好从板间射出的初速度为v0, 有
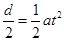?①? L＝v0t?②
得：a=?③? v0=2×107m/s?④
故电子入射速度v≥2×107m/s方能打到屏上。⑤
（2）要想离O最远，需要竖直速度最大，即在电场中加速时间最长，即水平速度最小，且竖直位移最大的电子打到屏上的距离最大。即恰能从极板边缘射出的电子打到屏上距O点最远。
离开电场时偏转量为?⑥
离开电场时的速度偏向角为??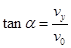⑦??⑧?
由几何关系?⑨
得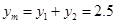：cm?（10）?
评分标准：每式1分
点评：难度中等，带电粒子在电场中的偏转常见于类平抛运动，根据水平和垂直两个分运动求解

本题难度：一般

3、计算题  如图，一个电子以速度v0=6.0×106m／s和仰角α=45°从带电平行板电容器的下板边缘向上板飞行。两板间场强E=2.0×104V／m，方向自下向上。若板间距离d=2.0×10-2m，板长L=10cm，问此电子能否从下板射至上板？它将击中极板的什么地方？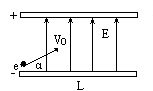

参考答案：见解析

本题解析：
【错解分析】错解：规定平行极板方向为x轴方向；垂直极板方向为y轴方向，将电子的运动分解到坐标轴方向上。由于重力远小于电场力可忽略不计，则y方向上电子在电场力作用下做匀减速运动，速度最后减小到零。
∵vt2-v02=2as? y=d=s? vt=0




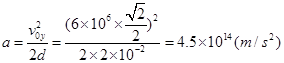
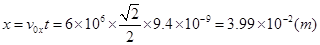
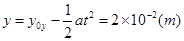
即电子刚好击中上板，击中点离出发点的水平位移为3.99×10-2（m）。
错解中，令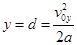来求加速度。这就意味着y方向的位移已经假定为d，（击中了上板）再求y为多少，就犯了循环论证的错误，修改了原题的已知条件。
【正解】应先计算y方向的实际最大位移，再与d进行比较判断。

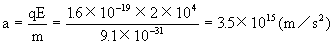
在y方向的最大高度为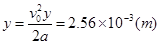
由于ym＜d，所以电子不能射至上板。

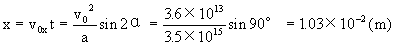
【点评】因此电子将做一种抛物线运动，最后落在下板上，落点与出发点相距1.03cm。
斜抛问题一般不要求考生掌握用运动学方法求解。用运动的合成分解的思想解此题，也不是多么困难的事，只要按照运动的实际情况把斜抛分解为垂直于电场方向上的的匀速直线运动，沿电场方向上的坚直上抛运动两个分运动。就可以解决问题。

本题难度：简单

4、选择题   将不带电的导体A和带有负电荷的导体B接触后，在导体A中的质子数 （?）
A．增加
B．减少
C．不变
D．先增加后减少

参考答案：C

本题解析：物体接触带电时，电子发生转移，导致相互接触的物体之间电荷不平衡，从而带电，而并非质子数目的变化，质子数目在接触过程中是不变的。C正确

本题难度：简单

5、计算题  在电场强度为E的匀强电场中，有两个质量均为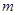的带电小球，带电量分别为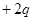和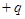，两小球用长为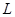的绝缘线相连，另用一根绝缘线系住带电为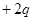的小球悬挂在O点而处于平衡状态，如图11所示。重力加速度为g。试确定：
（1）若电场方向竖直向下，悬线对悬点的作用力为多大？
（2）若电场水平向右，两段细线与竖直方向的夹角分别为多大？

参考答案：（1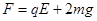）（2）

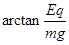
本题解析：（1）以两小球为研究对象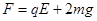，（2）以两小球为研究对象，所受电场力方向向右，大小为qE，绳子的拉力等于重力和电场力的合力，由力的合成可知上一段细线与竖直方向的夹角为，再以-q为研究对象，下一段绳子的拉力等于重力和向左的电场力的合力，可知细线与竖直方向的夹角为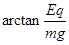
本题考查整体隔离法，当以两电荷为一个整体时，带电量为+q，分析上一段绳子的拉力，以-q为研究对象分析的是下一段绳子的拉力

本题难度：一般