1、简答题  汽车刹车前以10m/s的速度行驶，刹车后获得大小为2m/s2的加速度，则刹车后6秒的位移是多少？

参考答案：物体做匀减速直线运动，当速度减速为零时所需时间为：
t=v0a=10m/s2m/s2=5s，因此汽车在第6秒已经停止，故汽车6秒内的位移等于5秒内的位移，
因此有：
x=v0t+12at2=10m/s×5s+12(-2m/s2)×(5s)2=25m
故汽车在6秒内的位移大小为25m．

本题解析：

本题难度：一般

2、简答题  已知一物体做匀加速直线运动，加速度是a，请证明在一段时间t内的平均速度等于该段时间的中间t/2时刻的瞬时速度

参考答案：相等

本题解析：如图，设物体在A点的处速度为v0，从A到C的时间为t, B为从A到C的中间时刻，
则：S=V0t+(1/2)at2?
VB=V0+a(1/2)t?
V平均=S/t?
∴ VB= V平均?

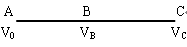
本题难度：简单

3、简答题  以某一速度沿正常的平直公路匀速行驶的汽车，进入冻雨路面后，交警提示司机必须以原速的一半行驶．司机发现，即使以原速的一半行驶，紧急刹车后的刹车距离仍然达到正常路面紧急刹车距离的两倍．已知该车在正常路面上刹车时的加速度大小为8m/s2，取g=10m/s2，求：
（1）汽车在正常路面上刹车时与地面间的动摩擦因数μ
（2）该车在冻雨路面上刹车时的加速度大小
（3）若汽车在冻雨路面上刹车距离不得超过8m，则汽车在冻雨路面上行驶的最大速度．

参考答案：（1）根据牛顿第二定律，有：μmg=ma
解得：μ=ag=8m/s210m/s2=0.8
（2）由题意知，在正常路面上时：0-V2=-2as，
在冻雨路面上时：0-（v2）2=-2a′×2s
解得：a′=a8=1m/s2．
（2）在冻雨路面上时：0-Vm2=-2a′s′，
得：Vm=

本题解析：

本题难度：一般

4、简答题  如图所示，跳伞运动员离开飞机后先做4s自由落体运动，后张开降落伞匀速下降4s，最后再做19s匀减速下降，着地时速度是2m/s，g取10m/s2．
（1）试作出运动员运动的v-t图象；
（2）求减速下降时的加速度（大小和方向）；
（3）求跳伞员离开直升飞机时距地面的高度．

参考答案：


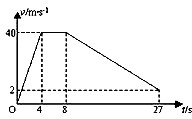
（1）跳伞运动员先做自由落体运动，加速度为g=10m/s2，4s末的速度为v=gt=40m/s．张开降落伞匀速下降的速度为40m/s，运动时间为4s．最后做19s匀减速下降，初速度为40m/s，末速度为2m/s．v-t图象如图所示．
（2）设运动员自由落体历时t1，匀速运动历时t2，减速运动历时t3，4s末的速度为vm，着地速度为v=2m/s，则
vm=gt1=40m/s
∴a=v-vmt3=2-4019m/s2=-2m/s2
负号表示方向竖直向上，加速度大小为2m/s2
（3）跳伞员离开飞机时的高度H=vm2t1+vmt2+vm+v2t3=639m
答：
（1）试作出运动员运动的v-t图象如图所示；
（2）减速下降时 的加速度方向竖直向上，大小为2m/s2；
（3）跳伞员离开直升飞机时距地面的高度是639m．

本题解析：

本题难度：一般

5、简答题  如图所示是建筑工地上常用的一种“深穴打夯机”。工作时，电动机带动两个紧压夯杆的滚轮匀速转动将夯杆从深为h的坑中提上来，当两个滚轮彼此分开时，夯杆被释放，最后夯杆在自身重力的作用下落回深坑，夯实坑底；然后两个滚轮再次压紧，夯杆再次被提上来，如此周而复始工作。已知两个滚轮边缘的线速度v恒为4m/s，每个滚轮对夯杆的正压力FN =2×104 N，滚轮和夯杆间的动摩擦因数μ =" 0.3" ，夯杆的质量m =1×10 3kg，坑深h ="6.4m" 。假定在打夯的过程中坑的深度变化不大，且夯的低端升到坑口时，速度正好为零。取g =10m/s2。试求：
（1）夯杆上升的过程中，被滚轮释放时它的速度为多大？
此时夯杆低端离坑底多高？
（2）每个打夯周期中，电动机对夯杆所做的功为多少？
（3）每个打夯周期中，由于摩擦产生的热量。
（4）打夯周期T.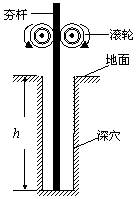

参考答案：（1）5.6 m?（2）6.4×104J?（3）3.9s

本题解析：（1）分析夯杆，由牛顿第二定律 2μFN –mg =ma?
当夯杆与滚轮速度相同时，v = at?
此时夯杆上升的高度h1 =" vt/2" = 4m?
当夯杆以v =" 4m/s" 初速度竖直上抛时，
上升的高度为h2 = v2/2g =" 0.8m" ，h 1 + h2 =" 4.8" m < h?
因此，夯杆先匀加速上升，后匀速上升，最后竖直上抛。
匀速上升的高度为h3 =" h" - h 1- h2 ?=" 1.6" m?
夯杆上升的过程中，被滚轮释放时它的速度为4m/s
此时夯杆低端离坑底 Δh =" h" – h2 =" 5.6" m?
(2) 由功能关系，每个打夯周期中，电动机对夯杆所做的功? w =" mgh" ="?" 6.4×104J?
(3) 夯杆先匀加速上升的时间 t=" v/a" = 2s?
滚轮的轮缘在相同时间内通过的路程为s? S =" vt" =" 8m?"
相对夯杆的路程为Δs =" s" – h1 =" 4m" ,?
产生的热量Q = 2μFN Δs = 4.8×104J?
（4）夯杆先匀加速上升的时间 t1 =" 2" s
匀速上升的时间 t2 = h3 /v = 0.4s?
被滚轮释放后到达最高点的时间为 t3 =" v/g" = 0.4s?
自最高点自由下落到坑底的时间为 t 4
由h = gt42 /2? t4 =" 1.1" s?
打夯周期T = t1 + t2 + t3+t4 = 3.9s

本题难度：一般