1、选择题 2012年10月25日,我国将第十六颗北斗卫星“北斗-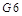 ”送入太空,并定点于地球静止轨道东经110.5°。由此,具有完全自主知识产权的北斗系统将首先具备为亚太地区提供高精度、高可靠定位、导航、授时服务,并具短报文通信能力。其定位精度优于20m,授时精度优于100ns。关于这颗“北斗-
”送入太空,并定点于地球静止轨道东经110.5°。由此,具有完全自主知识产权的北斗系统将首先具备为亚太地区提供高精度、高可靠定位、导航、授时服务,并具短报文通信能力。其定位精度优于20m,授时精度优于100ns。关于这颗“北斗-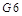 ”卫星以下说法中正确的有? (? )
”卫星以下说法中正确的有? (? )
A.这颗卫星轨道平面与东经110.5°的经线平面重合
B.通过地面控制可以将这颗卫星定点于成都正上方
C.这颗卫星的线速度大小比离地350公里高的天宫一号空间站线速度要大
D.这颗卫星的周期一定等于地球自转周期,轨道平面一定与赤道平面重合
参考答案:D
本题解析:地球同步卫星即地球同步轨道卫星,又称对地静止卫星,是运行在地球同步轨道上的人造卫星,其运行轨道是位于地球赤道平面上的圆形轨道,所以北斗导航卫星不可能与东经110.5°的经线平面重合,而成都不在赤道上,也不可能定点于成都正上方,故A、B错误,根据公式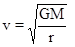 ,r越大,v越小.同步卫星距离地球的高度约为36000 km,其正常运行时的速度比离地350公里高的天宫一号空间站线速度小.故C错误;同步卫星运行周期与地球自转一周的时间相等均为24h,故D正确。
,r越大,v越小.同步卫星距离地球的高度约为36000 km,其正常运行时的速度比离地350公里高的天宫一号空间站线速度小.故C错误;同步卫星运行周期与地球自转一周的时间相等均为24h,故D正确。
本题难度:一般
2、实验题 如图甲所示,强强乘电梯速度为0.9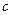 (
(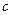 为光速)的宇宙飞船追赶正前方的壮壮,壮壮的飞行速度为0.5
为光速)的宇宙飞船追赶正前方的壮壮,壮壮的飞行速度为0.5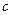 ,强强向壮壮发出一束光进行联络,则壮壮观测到该光束的传播速度为?。(填写选项前的字母)
,强强向壮壮发出一束光进行联络,则壮壮观测到该光束的传播速度为?。(填写选项前的字母)

A.0.4c
B.0.5c
C.0.9c
D.1.0c
参考答案:D
本题解析:根据爱因斯坦相对论,在任何参考系中,光速不变。D项正确。
本题难度:一般
3、选择题 宇宙中两颗相距很近的恒星常常组成一个双星系统,它们以相互间的万有引力彼此提供向心力,从而使它们绕着某一共同的圆心做匀速圆周运动,若已知它们的运转周期为T,两星到某一共同圆心的距离分别为R1和R2,那么,双星系统中两颗恒星的质量关系?
[? ]
A.这两颗恒星的质量必定相等
B.这两颗恒星的质量之和为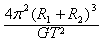
C.这两颗恒星的质量之比为m1:m2=R2:R1
D.其中必有一颗恒星的质量为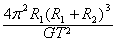
参考答案:BCD
本题解析:
本题难度:一般
4、选择题 嫦娥二号卫星于2010年成功发射,其环月飞行的高度距离月球表面100 km,所探测到的有关月球的数据比环月飞行高度为200 km的嫦娥一号更加详实.若两颗卫星环月飞行均可视为匀速圆周运动,飞行轨道如图所示.则

A.嫦娥二号环月飞行时角速度比嫦娥一号更小
B.嫦娥二号环月飞行的线速度比嫦娥一号更小
C.嫦娥二号环月飞行时向心加速度比嫦娥一号更小
D.嫦娥二号环月飞行的周期比嫦娥一号更小
参考答案:D
本题解析:考查万有引力定律与向心力公式,由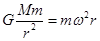 得到
得到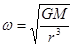 可知嫦娥二号环月飞行时角速度比嫦娥一号大,A错;由
可知嫦娥二号环月飞行时角速度比嫦娥一号大,A错;由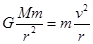 得到
得到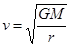 可知嫦娥二号环月飞行时线速度比嫦娥一号大,B错;由
可知嫦娥二号环月飞行时线速度比嫦娥一号大,B错;由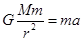 得到
得到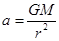 可知嫦娥二号环月飞行时向心加速度比嫦娥一号大,C错;由
可知嫦娥二号环月飞行时向心加速度比嫦娥一号大,C错;由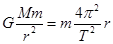 得到
得到 可知嫦娥二号环月飞行的周期比嫦娥一号小,D对。
可知嫦娥二号环月飞行的周期比嫦娥一号小,D对。
思路拓展:解此题时学生需注意嫦娥一号和嫦娥二号在绕月球做圆周运动时,都是月球对嫦娥一号和嫦娥二号的万有引力提供其运动的向心力。
本题难度:一般
5、选择题 课堂上老师给同学们布置了这样一个题目:假设地球是一半径为R,质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。求矿井底部和地球表面处的重力加速度大小之比。李明同学的思考过程如下: 由等式GM=gR2(G为引力常量,M为地球质量,R为地球半径,g为地球表面处的重力加速度)变形后得到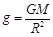 ,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比
,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比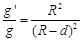 。下列说法中正确的是
。下列说法中正确的是
A.李明的答案是正确的
B.李明的答案是错误的,因为等式GM=gR2不成立
C.李明的答案是错误的,因为本题不能用等式GM=gR2求解
D.李明的答案是错误的,本题虽然能用等式GM=gR2求解,但他分析问题时出现错误
参考答案:D
本题解析:设地球的密度为ρ,则在地球表面,重力和地球的万有引力大小相等,有:g=G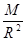 ,由于地球的质量为:M=
,由于地球的质量为:M=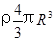 ?则地球表面的重力加速度:g=G
?则地球表面的重力加速度:g=G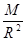
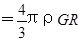 ,根据题意有,质量分布均匀的球壳对壳内物体的引力为零,在深度为d的井底,受到地球的万有引力即为半径等于(R-d)的球体在其表面产生的万有引力,故井底的重力加速度g=G
,根据题意有,质量分布均匀的球壳对壳内物体的引力为零,在深度为d的井底,受到地球的万有引力即为半径等于(R-d)的球体在其表面产生的万有引力,故井底的重力加速度g=G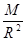
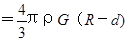 ,所以
,所以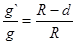 ,所以D正确。
,所以D正确。
本题难度:一般