1ΓΔ―Γ‘ώΧβ άϊ”ΟΚΫΧλΖ…ΜζΘ§”νΚΫ‘±Ω…“‘ΒΫΧΪΩ’÷–≥ωœ÷Ι ’œΒΡ»Υ‘λΒΊ«ρΈά–«…œΓΘ“―÷Σ“ΜΩ≈»Υ‘λΒΊ«ρΈά–«‘ΎάκΒΊΗΏΕ»“ΜΕ®ΒΡ‘≤ΙλΒά…œ‘Υ––ΓΘΒ±ΚΫΧλΖ…ΜζΫ”Ϋϋ’βΩ≈Έά–«≤Δ”κΥϋ‘Υ––«ιΩωΜυ±ΨœύΆ§ ±Θ§ΥΌΕ»¥οΒΫΝΥ6.4km®MsΓΘ»ΓΒΊ«ρΑκΨΕR=6400kmΘ§ΒΊ«ρ±μΟφ÷ΊΝΠΦ”ΥΌΕ»g=9.8m®Ms2Θ§«σ’βΩ≈Έά–«άκΒΊΟφΒΡΗΏΕ»ΓΘ
≤ΈΩΦ¥πΑΗΘΚ3400Km
±ΨΧβΫβΈωΘΚΩΦΒψΘΚ
Ή®ΧβΘΚΆρ”–“ΐΝΠΕ®¬…ΒΡ”Π”ΟΉ®ΧβΘ°
Ζ÷ΈωΘΚ¥ΥΧβΈΣΈά–«Ήω‘≤÷ή‘ΥΕ·ΒΡΜυ±ΨΦΤΥψ–ΆΧβΡΩΘ§Ϋη÷ζΆρ”–“ΐΝΠΕ®¬…ΚΆ‘ΥΕ·―ßΙΪ Ϋ’“≥ωΈά–«ΨύάκΒΊΟφΒΡΗΏΕ»ΚΆ≥ΘΝΩ÷°ΦδΒΡΙΊœΒΘΜΈΣΝΥ±ήΩΣΒΊ«ρ÷ ΝΩΈ ΧβΘ§Ω…“‘Ϋη÷ζ“ΜΒΊ«ρ±μΟφΡ≥ΈοΧεΒΡ÷ΊΝΠΩ…Ω¥Ήω «ΚΆΒΊ«ρ÷°ΦδΒΡΆρ”–“ΐΝΠ»ΞΫβΨωΘ°
Ϋβ¥πΘΚΫβΘΚ…ηΒΊ«ρ÷ ΝΩMΘ§ΒΊ«ρΑκΨΕRΘ§Έά–«ΨύάκΒΊΟφΗΏΕ»hΘ§Έά–«÷ ΝΩmΘ§Β±ΚΫΧλΖ…ΜζΫ”Ϋϋ’βΩ≈Έά–«≤Δ”κΥϊ‘Υ––«ιΩωΜυ±ΨœύΆ§ ±Θ§ΥΌΕ»¥οΒΫΝΥv=6.4km/sΘ§ΥΒΟςΈά–«ΒΡ‘Υ––ΥΌΕ»“≤ «v=6.4km/sΘ§Έά–«‘ΎΧλ…œ ±Θ§”…Άρ”–“ΐΝΠΧαΙ©œρ–ΡΝΠΘ§Υυ“‘ΘΚG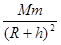 =m
=m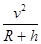 ?
?
ΉΣΜΜΙΪ ΫΩ…ΒΟΘΚv2=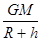 ?ΔΌΘ§Νμ…ηΒΊ«ρ±μΟφ…œ”–“ΜΈοΧεΘ§÷ ΝΩΈΣm1Θ§Ρ«Ο¥Υϋ‘ΎΒΊ«ρ±μΟφ ήΒΫΒΡΆρ”–“ΐΝΠΨΆ «Τδ÷ΊΝΠΥυ“‘Θ§m1g=G
?ΔΌΘ§Νμ…ηΒΊ«ρ±μΟφ…œ”–“ΜΈοΧεΘ§÷ ΝΩΈΣm1Θ§Ρ«Ο¥Υϋ‘ΎΒΊ«ρ±μΟφ ήΒΫΒΡΆρ”–“ΐΝΠΨΆ «Τδ÷ΊΝΠΥυ“‘Θ§m1g=G Θ§ ΉΣΜΜΙΪ ΫΩ…ΒΟΘΚGM=R2g?ΔΎ
Θ§ ΉΣΜΜΙΪ ΫΩ…ΒΟΘΚGM=R2g?ΔΎ
ΫΪΔΎ¥ζ»κΔΌΒΟΒΫΘΚv2=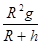 ?Φ¥?h=
?Φ¥?h=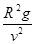 -RΘ§ΫΪ“―÷Σ ΐΨί¥ζ»κΘ§ΒΟΒΫΘΚh="3400km"
-RΘ§ΫΪ“―÷Σ ΐΨί¥ζ»κΘ§ΒΟΒΫΘΚh="3400km"
Ι ’βΩ≈Έά–«άκΒΊΟφΒΡΗΏΕ»ΈΣ3400km
ΒψΤάΘΚ¥ΥΧβΈΣΈά–«Ήω‘≤÷ή‘ΥΕ·ΒΡΜυ±ΨΦΤΥψ–ΆΧβΡΩΘ§÷ς“ΣΩΦ≤ιΆρ”–“ΐΝΠ≥δΒ±œρ–ΡΝΠΒΡœύΙΊ”Π”ΟΚΆΦΤΥψΘ§ΈΣ÷–ΒΒΧβΘ°
±ΨΧβΡ―Ε»ΘΚΦρΒΞ
2ΓΔΦΤΥψΧβ (8 Ζ÷Θ©.“―÷ΣΒΊ«ρΆ§≤ΫΈά–«άκΒΊΟφΒΡΗΏΕ»‘ΦΈΣΒΊ«ρΑκΨΕΒΡ6±ΕΓΘ»τΡ≥–––«ΒΡΤΫΨυΟήΕ»ΈΣΒΊ«ρΤΫΨυΟήΕ»ΒΡ“ΜΑκΘ§ΥϋΒΡΆ§≤ΫΈά–«ΨύΤδ±μΟφΒΡΗΏΕ» «ΤδΑκΨΕΒΡ2.5±ΕΘ§«σΘΚΗΟ–––«ΒΡΉ‘ΉΣ÷ήΤΎΓΘ
≤ΈΩΦ¥πΑΗΘΚ12h
±ΨΧβΫβΈωΘΚΒΊ«ρΒΡΆ§≤ΫΈά–«ΒΡ÷ήΤΎΈΣT1=24–Γ ±Θ§ΙλΒάΑκΨΕΈΣr1=7R1Θ§ΟήΕ»Π―1ΓΘΡ≥–––«ΒΡΆ§≤ΫΈά–«÷ήΤΎΈΣT2Θ§ΙλΒάΑκΨΕΈΣr2=3.5R2Θ§ΟήΕ»Π―2ΓΘΗυΨί≈ΘΕΌΒΎΕΰΕ®¬…ΚΆΆρ”–“ΐΝΠΕ®¬…Ζ÷±π”–
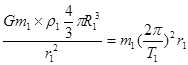 ?Θ®3Ζ÷Θ©
?Θ®3Ζ÷Θ©
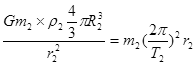 ?Θ®3Ζ÷Θ©
?Θ®3Ζ÷Θ©
ΝΫ ΫΜ·ΦρΒΟ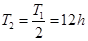 ?Θ®2Ζ÷Θ©
?Θ®2Ζ÷Θ©
±ΨΧβΡ―Ε»ΘΚ“ΜΑψ
3ΓΔ―Γ‘ώΧβ …ηΡ≥“Μ–««ρ¥χΗΚΒγΘ§“ΜΒγΉ”Ζέ≥Ψ–ϋΗΓ‘ΎΨύ–««ρ±μΟφΈΣRΒΡΒΊΖΫΘ§œ÷ΫΪΗΟΒγΉ”Ζέ≥Ψ“ΤΒΫΨύ–««ρ±μΟφ2RΒΡΒΊΖΫœύΕ‘”ΎΗΟ–««ρΈό≥θΥΌΒΊ ΆΖ≈Θ§‘ρΒγΉ”Ζέ≥ΨΫΪΘ®ΓΓΓΓΘ©
AΘ°œρ–««ρœ¬¬δ
BΘ°»‘‘Ύ‘≠¥Π–ϋΗΓ
CΘ°ΆΤœρΧΪΩ’
DΘ°ΈόΖ®≈–Εœ
≤ΈΩΦ¥πΑΗΘΚΒ±¥χΗΚΒγΖέ≥Ψ‘ΎΗΏΕ»ΈΣR¥Π¥Π”ΎΤΫΚβΘ°‘ρ”–
GmM(r+R)2=kqQ(r+R)2Θ§rΈΣ–««ρΒΡΑκΨΕΘ°
Β±R±δ2R ±Θ§ΝΫΝΠ»‘»ΜΤΫΚβΘ°
Ι ―ΓBΘ°
±ΨΧβΫβΈωΘΚ
±ΨΧβΡ―Ε»ΘΚ“ΜΑψ
4ΓΔΦΤΥψΧβ Θ®10Ζ÷Θ©ΓΑφœΕπ±Φ‘¬Γ±ΒΡΙΐ≥ΧΩ…“‘ΦρΜ·ΈΣΘΚΓΑφœΕπ“ΜΚ≈Γ±…ΐΩ’ΚσΘ§»ΤΒΊ«ρ―ΊΆ÷‘≤ΙλΒά‘ΥΕ·Θ§‘ΕΒΊΒψAΨύΒΊΟφΗΏΈΣh1?Θ§‘Ύ‘ΕΒΊΒψ ±ΒΡΥΌΕ»ΈΣvΘ§»ΜΚσΨ≠Ιΐ±δΙλ±Μ‘¬«ρ≤ΕΜώΘ§‘ΌΨ≠Εύ¥Έ±δΙλΘ§Ήν÷’‘ΎΨύάꑬ«ρ±μΟφΗΏΈΣh2ΒΡΙλΒά…œ»Τ‘¬«ρΉω‘»ΥΌ‘≤÷ή‘ΥΕ·ΓΘ
Θ®1Θ©“―÷ΣΒΊ«ρΑκΨΕΈΣR1Θ°±μΟφΒΡ÷ΊΝΠΦ”ΥΌΕ»ΈΣg0Θ§«σΓΑφœΕπ“ΜΚ≈Γ±‘Ύ‘ΕΒΊΒψA¥ΠΒΡΦ”ΥΌΕ»aΘΜ
Θ®2Θ©“―÷Σ‘¬«ρΒΡ÷ ΝΩΈΣMΘ°ΑκΨΕΈΣR2Θ§“ΐΝΠ≥ΘΝΩΈΣGΘ§«σΓΑφœΕπ“ΜΚ≈Γ±»Τ‘¬«ρ‘ΥΕ·ΒΡ÷ήΤΎTΓΘ
≤ΈΩΦ¥πΑΗΘΚΘ®1Θ©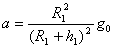 ?Θ®2Θ©
?Θ®2Θ©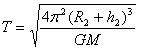
±ΨΧβΫβΈωΘΚΘ®1Θ©…η“ΐΝΠ≥ΘΝΩΈΣGΘ§ΒΊ«ρ÷ ΝΩΈΣM1Θ§ΓΑφœΕπ“ΜΚ≈Γ±Έά–«
ΒΡ÷ ΝΩΈΣmΘ§”…≈ΘΕΌΒΎΕΰΕ®¬…”–ΘΚ?
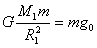 ?ΔΌ
?ΔΌ
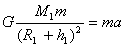 ?ΔΎ
?ΔΎ
ΫβΒΟΘΚ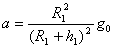 ?Δέ
?Δέ
Θ®2Θ©ΓΑφœΕπ“ΜΚ≈Γ±»Τ‘¬«ρ‘Υ–– ±Θ§”–ΘΚ
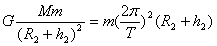 ?Δή
?Δή
ΫβΒΟΘΚ 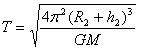 ?Δί
?Δί
ΤάΖ÷±ξΉΦΘΚ±ΨΧβΙ≤10Ζ÷ΓΘΤδ÷–Θ§ΔΌΔΎΔέΔήΔίΟΩ Ϋ2Ζ÷ΓΘ
±ΨΧβΩΦ≤ιΆρ”–“ΐΝΠΕ®¬…ΒΡ”Π”ΟΘ§‘Ύ–««ρ±μΟφ÷ΊΝΠ”κΆρ”–“ΐΝΠœύΒ»Θ§”…¥ΥΩ…«σΒΟGMΒΡ÷ΒΘ§”…‘ΎΗΏΕ»h1ΈΜ÷Ο”…Άρ”–“ΐΝΠΧαΙ©œρ–ΡΝΠΩ…«σΒΟœρ–ΡΦ”ΥΌΕ»¥σ–ΓΘ§ΓΑφœΕπ“ΜΚ≈Γ±»Τ‘¬«ρ‘Υ–– ±Θ§”–Άρ”–“ΐΝΠΧαΙ©œρ–ΡΝΠΘ§ΗυΨί÷ήΤΎΙΪ ΫT=2Π–/wΩ…«σΒΟ÷ήΤΎ¥σ–Γ
±ΨΧβΡ―Ε»ΘΚ“ΜΑψ
5ΓΔ―Γ‘ώΧβ ‘Ύ≈ΘΕΌΖΔ±μΆρ”–“ΐΝΠΕ®¬…“ΜΑΌΕύΡξ÷°ΚσΘ§Ω®ΈΡΒœ–μ Ήœ»ΨΪ»Ζ≤βΝΩΝΥ“ΐΝΠ≥ΘΝΩΘ°‘ΎΙζΦ ΒΞΈΜ÷Τ÷–“ΐΝΠ≥ΘΝΩΒΡΒΞΈΜ «Θ®ΓΓΓΓΘ©
AΘ°N?kg2
BΘ°N?m2
CΘ°N?kg2/m2
DΘ°N?m2/kg2
≤ΈΩΦ¥πΑΗΘΚD
±ΨΧβΫβΈωΘΚ
±ΨΧβΡ―Ε»ΘΚΦρΒΞ