1、选择题  不定项选择
两名质量相等的滑冰人甲和乙都静止在光滑的水平冰面上，现在，其中一人向另一个人抛出一个篮球，另一人接球后再抛回，如此反复进行几次后，甲和乙最后的速率关系是（ ? ）
A．若甲最先抛球，则一定是v甲＞v乙
B．若乙最后接球，则一定是v甲＞v乙
C．只有甲先抛球，乙最后接球，才有v甲＞v乙
D．无论怎样抛球和接球，都是v甲＞v乙

参考答案：B

本题解析：

本题难度：一般

2、实验题  某同学设计了一个用打点计时器验证动量守恒定律的实验：在小车A的前端粘有橡皮泥，推动小车A使之做匀速直线运动，然后与原来静止在前方的小车B相碰并粘合成一体，继续做匀速直线运动。他设计的具体装置如图所示，在小车A后连着纸带，打点计时器的频率为50HZ，长木板下垫有小木片用来平衡摩擦力。
（1）若已得到的纸带如图所示并已测得计数点间的距离，A为运动起始的第一点，则应选______段计算A的碰前的速度。（填“AB”或“BC”、“CD”或”DE”）
（2）已测得的小车A的质量mA=0.40kg，小车B的质量mB=0.20kg由以上的测量可得：碰后两小车的总动量为_________kg.m/s。

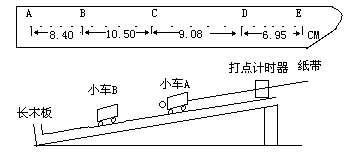
参考答案：（1）BC
（2）0.417

本题解析：

本题难度：一般

3、简答题  
（1）物块A与B发生碰撞。
（2）物块A与B发生碰撞（设为弹性碰撞）后，物块B与档板P发生碰撞。
（3）物块B与档板P发生碰撞（设为弹性碰撞）后，物块B与A在木板C上再发生碰撞。
（4）物块A从木板C上掉下来。
（5）物块B从木板C上掉下来。

参考答案：
（1）A与B发生碰撞的条件是：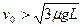
(2) A与B相撞，B再与P相撞的条件是：
(3)物块A的初速度?时, 物块B、A在木板C上不可能再发生碰撞
(4) A从C掉下的条件是：
( 5)物块B从木板C上掉下的条件是：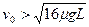

本题解析：用m表示A、B和C的质量。
（1）当物块A以初速度v0向右运动时，它因受C给它的滑动摩擦力做匀减速直线运动，而它作用于C的摩擦力不足以使B、C产生相对滑动，即B、C以相同加速度做匀加速直线运动。物块A、B发生碰撞的临界情况是：物块A运动到物块B所在处时，A、B速度相等。
在临界状况下，因为B与木板C的速度始终相等，所以A、B即将碰撞时，A、B、C三者速度均相同，设为v1。由动量守恒定律有
mv0=3mv1?①
在此过程中，设木板C 运动的路程为s1，则物块A运动的路程为s1+L，由功能原理得：
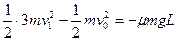?②
解①、②得：??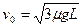
故A与B发生碰撞的条件是：?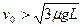
（2）当物块A的初速度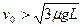时，A、B将发生碰撞，物块B与档板P发生碰撞的临界情况是：物块B运动到档板P所在处时，B、C的速度相等。同（1）中结论，在临界状况下，当B运动到档板P处时，A、B、C三者速度相等，设此速度为v2，根据动量守恒定律得：
mv0＝3mv2?③
设A、B碰撞前瞬间，A、B、C速度分别为vA、vB和vC，则vA>vB，vB=vC。
在A、B碰撞的极短时间内，A、B构成的系统的动量近似守恒，而木板C的速度保持不变，因为A、B间的碰撞是弹性的，即系统机械能守恒，又物块A、B质量相等，故易得：碰撞后A、B速度交换，设碰撞刚结束时A、B、C三者的速度分别为vAˊ、vBˊ、vCˊ，则vAˊ＝vB，vBˊ＝vA，vCˊ＝vC，刚碰撞后A、B、C的运动与（1）类似，只是A、B的运动进行了交换，由此易分析：在整个运动过程中，先是A相对C运动的路程为L，接着是B相对C运动的路程为L，整个系统的动能转变为内能。类似（1）中方程得
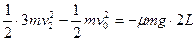?④?
联立③、④解之，得：
故A与B相撞，B再与P相撞的条件是：
（3）当物块A的初速度?时，B将与档板P相撞，撞后A、B、C的运动可由（2）中运动类比得到：B、P碰撞后瞬间，物块A、B速度相同，木板C速度最大，然后C以较大的加速度向右做减速运动，而物块A和B以相同的较小加速度向右做加速运动，加速过程将持续到或者A、B与C速度相同，三者以相同速度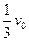向右做匀速运动，或者木块A从木板C上掉了下来，因此物块B、A在木板C上不可能再发生碰撞。
(4)若A刚刚没从木板C上掉下来，即A到达C的左端时的速度变为与C相同，这时三者的速度皆相同，以v3表示，由动量守恒有
? 3mv3=mv0?⑤
从A以初速度v0在木板C的左端开始运动，经过B与P相碰，直到A刚没从木板C的左端掉下来，这一整个过程中，系统内部先是A相对C运动的路程为L，接着B相对C运动的路程也是L，B与P碰后直到A刚没从木板C上掉下来，A与B相对C运动的路程也皆为L，整个系统动能的改变应等于内部相互滑动摩擦力做功的代数和。
即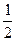：(3m)v32-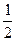mv02 =-μmg·4L?⑥
由⑤⑥两式得：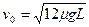
故A从C掉下的条件是：
（5）当物块A的初速度时，A将从木板C上掉下来。设A刚从木板C上掉下来时，A、B、C三者的速度分别为vA″, vB″, vC″，有vA″＝vB″＜vC″，这时⑤式应改写成
mv0=2m vA″+mvC″?⑦
⑥式应改写成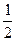：?(2m)vB″2+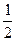mv″C2-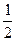mv0=-μmg·4L?⑧
当物块A掉下C后，物块B从木板C掉下的临界情况是：当C在左端赶上B时，B与C的速度相等，设此速度为v4
则由动量守恒定律可得：?mvB″+ mvC″＝2mv4?⑨
再对B、C系统从A掉下C到B掉下C的过程用动能定律：
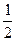(2m)v42 —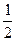（mv″B2+mvC″2）= -μmgL?⑩
联立⑦⑧⑨⑩，注意到vA″＝vB″＜vC″，可解得：
，，

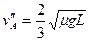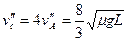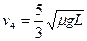
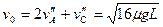
故物块B从木板C上掉下的条件是：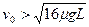

本题难度：一般

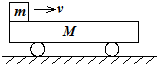
4、选择题  M置于光滑平面上，上表面粗糙且足够长，木块m以初速度v滑上车表面，则（　　）
A．m的最终速度为