1、计算题  放在水平地面上的一物块，受到方向不变的水平推力F的作用，F的大小与时间t的关系和物块速度v与时间t的关系如图所示。取重力加速度g＝10m/s2。求：
（1）物块在运动过程中受到的滑动摩擦力；
（2）物块的质量m；
（3）物块与地面之间的动摩擦因数μ。

参考答案：解：（1）物体在4s-6s做匀速运动，则f=F3=2N
（2）由速度图象可知，2s-4s物体加速度为
由牛顿第二定律得：F3-f= ma
解得：m＝0.5kg
（3）f=μN=μmg
得：μ＝0.4

本题解析：

本题难度：一般

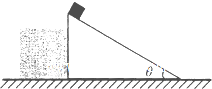
2、简答题  如图所示，倾角为θ的斜面体与正方体靠在一起置于水平面上，一质量为m的滑块从斜面的顶端由静止开始滑到斜面底端，此过程中正方体始终处于静止状态．已知斜面体的底面光滑，斜面部分与滑块间的动摩擦因数为μ，斜面体的高度为h，重力加速度大小为g，求：
（l）滑块沿斜面下滑的时间；
（2）正方体所受地面摩擦力的大小．

参考答案：（1）滑块下滑时，由牛顿第二定律得：
mgsinθ-μmgcosθ=ma，
由匀变速运动的位移公式得：
hsinθ=12at2，
解得：t=

本题解析：

本题难度：一般

3、选择题  如图，传送带两轮间距为L，传送带运动速度为v0，今在其左端静止地放一个木块，设木块与传送带之间的动摩擦因数为μ，放上木块后传送带速率不受影响，则木块从左端运动到右端的时间可能为

[? ]
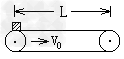
A、?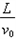
B、?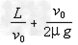
C、?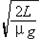
D、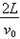

参考答案：BCD

本题解析：

本题难度：一般

4、计算题  如图1所示，质量m=1.0kg的物块，在水平向右、大小F = 5.0N的恒力作用下，沿足够长的粗糙水平面由静止开始运动。在运动过程中，空气对物块的阻力沿水平方向向左，其大小f空=kv，k为比例系数，f空随时间t变化的关系如图2所示。g取10m/s2。

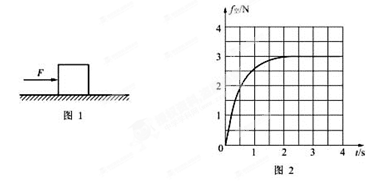
（1）求物块与水平面间的动摩擦因数μ；
（2）估算物块运动的最大速度vm；
（3）估算比例系数k。

参考答案：（1）?（2）?（3）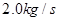

本题解析：（1）由图2可知，2s后空气对物块的阻力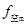大小不变，即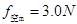，物块做匀速直线运动，设水平面对物块的摩擦力为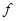，由平衡条件得：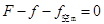
又因为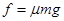　　
联立解得：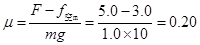
（2）因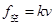随速度的增大而增大，而恒力F和水平面对物块的摩擦力为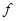保持不变，所以在内，物块做加速度逐渐减小的加速运动，匀速运动时速度达到最大，根据动量定理有

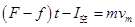
在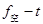图象中，图线与横轴围成的“面积”表示冲量，设每个小正方形的面积为，由图2可知，在内，图线与横轴围成的的“面积”内含有小正方形的个数为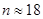，则

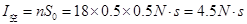
所以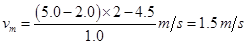　
（3）因为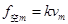，所以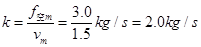

本题难度：一般

5、计算题  如图10甲所示，一根质量可以忽略不计的轻弹簧，劲度系数为k，下面悬挂一个质量为m的砝码A。手拿一块质量为M的木板B，用木板B托住A向上压缩弹簧到一定程度，如图乙所示。此时如果突然撤去木板B，则A向下运动的加速度a（a>g）。现用手控制使B以加速度a/3向下做匀加速直线运动。（1）求砝码A做匀加速直线运动的时间。（2）求出这段运动过程的起始和终止时刻手对木板B的作用力大小的表达式。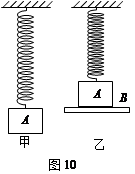

参考答案：（1）；（2）M（g-a/3）。

本题解析：（1）设最初弹簧被压缩的长度为x0，根据牛顿第二定律对A有kx0+mg=ma
解得x0=m（a-g）/k
设A和B以加速度a/3向下做匀加速运动过程的终止时刻弹簧的压缩量为x1，根据牛顿第二定律对A有? kx1+mg=ma/3?
解得x1=m（a/3-g）/k
设A和B一起做匀加速运动的时间为t1，在这段时间内，A运动的位移为
s=x0-x1
根据s=，可解得?
（2）起始时刻A受三个力，满足mg+kx0-N1="ma/3"
B受三个力，满足Mg+N1-F1="Ma/3"
解得：F1=M（g-a/3）+2ma/3
A与B脱离时B受二个力，满足Mg-F2=Ma/3
解得：F2= M（g-a/3）

本题难度：一般