1、选择题 可发射一颗人造卫星,使其圆轨道满足下列条件(?)
A.与地球表面上某一纬度线(非赤道)是共面的同心圆
B.与地球表面上某一经度线始终是共面的同心圆
C.与地球表面上的赤道线是共面同心圆,且卫星相对地面是运动的
D.与地球表面上的赤道线是共面同心圆,且卫星相对地面是静止的
参考答案:CD
本题解析:卫星在圆轨道上绕地球运行时,万有引力提供向心力,故圆周运动的圆心应在地球的中心.
A、卫星在圆轨道上绕地球运行时,一个最明显的特点是轨道的圆心是地心,而万有引力总是地心与卫星连线方向上的,所以卫星轨道平面必过地心.故A错误.
B、卫星通过南北极上空,某时刻在某一经线上,由于地球的自转下一时刻卫星将不在原来的经线上,故B错误.
C、与地球表面上赤道线是共面同心圆,卫星相对地面是静止的,该卫星是同步卫星,周期与地球自转周期相同,故C正确.
D、与地球表面上赤道线是共面同心圆,周期与地球自转周期不相同,卫星相对地面是运动的,故D正确.
故选CD
点评:人造卫星做圆周运动是万有引力提供向心力,故圆周运动的圆心应在地球的中心.卫星是相对地心作圆周运动,而经线是相对地轴随时转动的.也就是说,相对地心来说,经线是一直转动的,而极低卫星则不然.因此是找不到这样的卫星的.
本题难度:简单
2、选择题 两颗人造地球卫星,质量之比m1:m2=1:2,轨道半径之比R1:R2=3:1,下面有关数据之比正确的是
A.周期之比T1:T2=3:1
B.线速度之比v1:v2=1: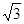
C.向心力之比为F1:F2=1:9
D.向心加速度之比a1:a2=1:9
参考答案:BD
本题解析:根据万有引力提供向心力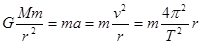 ,解得a=
,解得a= 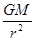 ,v=
,v= 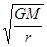 ,T=
,T=  .可知周期之比T1:T2=
.可知周期之比T1:T2=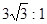 ,线速度之比v1:v2=1:
,线速度之比v1:v2=1: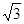 。向心加速度之比a1:a2=1:9.向心力等于万有引力,等于F=
。向心加速度之比a1:a2=1:9.向心力等于万有引力,等于F=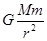 。则向心力之比为1:18.故选BD
。则向心力之比为1:18.故选BD
点评:本题难度较小,熟练掌握万有引力提供向心力中线速度、角速度、周期公式
本题难度:一般
3、选择题 从地球上发射两颗人造地球卫星A和B,绕地球做匀速圆周运动的半径之比为RA:RB=4:1,则它们的线速度之比υA:υB和运动周期之比TA:TB为( )
A.2:1,1:16
B.1:2,8:1
C.1:2,1:8
D.2:1,2:1
参考答案:1、人造卫星受到地球的万有引力提供向心力,即:GMmr2=mv2r,所以v=
本题解析:
本题难度:简单
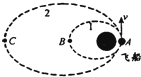
4、选择题 2007年10月25日17时55分,北京航天飞行控制中心对“嫦娥一号”卫星实施首次变轨控制并获得成功.这次变轨是在卫星运行到远地点时实施的,而此后将要进行的3次变轨均在近地点实施.“嫦娥一号”卫星的首次变轨之所以选择在远地点实施,是为了抬高卫星近地点的轨道高度.同样的道理,要抬高远地点的高度就需要在近地点实施变轨.如图为“嫦娥一号”某次在近地点A由轨道1变轨为轨道2的两个轨道的示意图,其中B、C分别为两个轨道的远地点.关于上述变轨过程及“嫦娥一号”在两个轨道上运动的情况,下列说法中正确的是( )
A.“嫦娥一号”在轨道1的A点处应点火加速
B.“嫦娥一号”在轨道1的A点处的速度比在轨道2的A点处的速度大
C.“嫦娥一号”在轨道1的B点处的加速度比在轨道2的C点处的加速度小
D.以上说法都不对