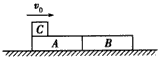
1、计算题  如图所示，在光滑水平面上有两个并排放置的木块A、B，已知mA=0.5kg，mB=0.3 kg。现有质量m0=0.08 kg的小物块C以初速v0=25m/s在A表面沿水平方向向右滑动，由于C与A、B间均有摩擦，C最终停在B上，B、C最后的共同速度v=2.5 m/s。求：
(1)A木块的最终速度的大小；
(2)C物块滑离A木块的瞬时速度大小。

参考答案：解：小物块C沿木块A表面滑动时，A对C的摩擦力使C做减速运动，使A、B共同做加速运动；C滑上B后，C继续做减速运动，B继续加速，A匀速运动，A、B开始分离，直至C、B达到共同速度，然后C、B一起做匀速运动，在上述过程中，A、B、C构成的系统所受的合外力为零，系统的动量守恒。设木块A的最终速度为v1，C滑离A时的速度为v2，由动量守恒定律，则
(1)对A、B、C有m0v0=mAv1+（mB+m0）v，解得v1=2.1m/s
(2)当C滑离A后，对B、C有m0v2+mBv1=(mB+m0)v
或对A、B、C有m0v0=（mA+mB）v1+m0v2
解得v2=4 m/s

本题解析：

本题难度：一般

2、选择题  质量为M的木块在光滑水平面上以速率v1向右运动，质量为m的子弹以速率v2水平向左射入木块，假设子弹射入木块后均未穿出，且在第N颗子弹射入后，木块恰好停下来，则N为
[? ]
A.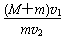
B.
C.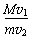
D.?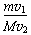

参考答案：C

本题解析：

本题难度：一般

3、选择题  将质量为m1的物块P（可视为质点）从置于光滑水平面上的斜面体Q（质量m2）的顶端由静止释放。由于斜面体各处粗糙程度不同，最后恰好滑到Q的底端与之相对静止。如图所示.已知Q底边长为a，倾角为θ。对于上述过程，由P和Q组成的系统下述说法正确的是（?）

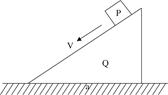
A．动量守恒
B．机械能守恒
C．最后P和Q以一定的速度共同向左运动
D．物块Q对地位移为m1a/(m1+m2)

参考答案：D

本题解析：略

本题难度：简单

4、计算题  （9分）如图所示，光滑的水平面上静止着半径相同的三个小球A、B、C，其中小球A、C的质量分别为mA=m、mC=4m。现使A以初速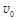沿B、C的连线方向向B运动，求B球的质量M为何值时，才能使C球碰撞后的速度最大？（已知A、B、C之间的碰撞均为弹性碰撞）

参考答案：2m

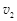本题解析：以碰撞前A球的速度方向为正，A球与B球发生弹性碰撞，设碰撞后的速度分别为和，由能量守恒定律和动量守恒定律，得
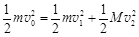? 1分
? 1分
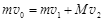解得　? 1分
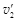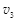B球与C球发生弹性碰撞，设碰撞后的速度分别为和，由能量守恒定律和动量守恒定律，得
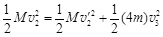? 1分
? 1分
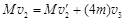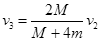解得　? 1分
故C球碰撞后的速度
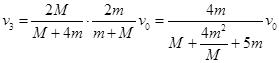? 1分
由数学关系解得时，C球碰撞后的速度最大。? 2分

本题难度：一般

5、简答题  一质量为M的长木板静止在光滑水平桌面上．一质量为m的小滑块以水平速度v0从长木板的一端开始在木板上滑动，直到离开木板．滑块刚离开木板时的速度为v0/3．若把该木板固定在水平桌面上，其它条件相同，求滑块离开木板时的速度v．

参考答案：设第一次滑块离开时木板速度为v，由系统的动量守恒，有
mvo=m?v03+Mv，
解得v=2mv03M
设滑块与木板间摩擦力为f，木板长L，滑行距离s，如图，

由动能定理对木板：fs=12Mv2　　　
对滑块：-f（s+L）=12m(v03)2-12mv20
即fL=12mv20-12m(v03)2-12Mv2　
当板固定时　fL=12mv20-12mv′2
解得v′=v03

本题解析：

本题难度：一般