1、选择题 如图所示,弹簧秤外壳质量为m,弹簧及挂钩的质量忽略不计,挂钩上吊一重物。现用一竖直向上的外力拉弹簧秤,当弹簧秤向上做匀速直线运动时,示数为F1;若让弹簧秤以加速度a向上做匀加速直线运动,则弹簧秤的示数为(重力加速度为g.不计空气阻力)
A.mg
B.F1 + mg
C.F1 + ma
D.
参考答案:D
本题解析:
本题考查平衡条件;牛顿第二定律;胡克定律。解答本题的关键是知道弹簧秤的示数等于弹簧秤对重物拉力的大小;对重物受力分析,求出重物质量,进而弹簧的拉力。
设重物的质量为M,对重物受力分析,受重力Mg和弹簧的拉力F。当弹簧秤向上做匀速直线运动时,由平衡条件知: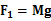 ?。当弹簧秤以加速度a向上做匀加速直线运动时,根据牛顿第二定律得:
?。当弹簧秤以加速度a向上做匀加速直线运动时,根据牛顿第二定律得: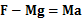 ?,以上两式联立解得:
?,以上两式联立解得: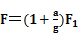 ?,故D正确。
?,故D正确。
本题难度:一般
2、计算题 (10分)如图所示,质量为m的物体放在水平桌面上。在水平恒力F作用下,速度由v1增大到v2的过程中,发生的位移为s。已知物体与水平桌面的动摩擦因数为μ,重力加速度为g。

(1)分别求出水平恒力F和摩擦力所做的功;
(2)若此过程中合外力所做的功用W合表示,物体动能的增量用ΔEk表示,证明W合=ΔEk。
参考答案:(1)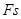 ?
?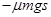 ?(2)过程见解析
?(2)过程见解析
本题解析:
(1)水平恒力与位移方向相同,所以水平恒力所做的功?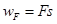
摩擦力方向与位移方向相反,摩擦力所做的功?
(2)物体在合外力作用下做匀加速直线运动,有
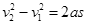
由牛顿第二定律,合外力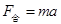 ?
?
合外力对物体所做的功? ?
?
本题难度:一般
3、计算题 (7分)质量m=0.40kg的物体静止在水平地面上,其与地面间的动摩擦因数?=0.20。现用水平向右的外力F=1.0N推物体,求:(1)物体2.0s末的速度多大;(2)前2.0s内外力F做多少功;(3)若2.0s末撤去外力,物体还要经过多长时间才能停下来。
参考答案:(1)设物体做匀加速直线运动的加速度为a1,根据牛顿第二定律有
F-μmg=ma1,解得a1=0.50m/s2…………………………………………(2分)
物体2.0s末的速度大小v=a1t1="1.0m/s" ……………………………………(1分)
(2)前2.0s内的位移大小s=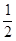 a1t12=1.0m………………………………………(1分)
a1t12=1.0m………………………………………(1分)
所以前2.0s内外力F所做的功W="Fs=1.0J" …………………………………(1分)
(3)设撤去外力后物体运动的加速度为a2,根据牛顿第二定律有
μmg=ma2,解得? a2=2.0m/s2…………………………………………………(1分)
物体运动的时间t2=v/a2="0.50s" …………………………………………………(1分)
本题解析:(1)直接根据牛顿第二定律、加速度和速度关系公式可正确解答.
(2)根据运动公式求出位移,利用做功公式求解。
(3)撤掉拉力后,物体在摩擦力作用下减速前进,根据牛顿第二定律可以求出物体的加速度,然后根据运动学公式可以求出物体滑动的距离.
本题难度:一般
4、选择题 如图1所示,mA=4.Okg,mB=2.Okg,A和B紧靠着放在光滑水平面上,从t=O时刻起,对B施加向右的水平恒力F2=4.ON,同时对A施加向右的水平变力F1,F1变化规律如图2所示.下列相关说法中正确的是( )
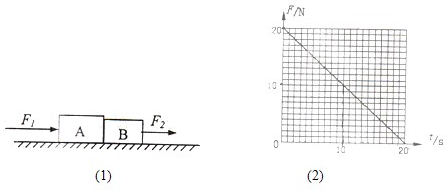
A.当t=0时,A、B物体加速度分别为aA=5m/s2,aB=2m/s2
B.A物体作加速度减小的加速运动,B物体作匀加速运动
C.t=12?s时刻A、B将分离,分离时加速度均为a=2m/s2
D.A、B分离前后,A物体加速度变化规律相同
参考答案:若AB之间没有力的作用,则aB=F2mB=2m/s2,
A、当t=0时,F1=2ON,而mA=4.Okg,所以F1单独作用在A上的加速度大于AB之间没有力的作用时的加速度,此时AB一起运动,加速度为:a=F合mA+mB=246=4m/s2,故A错误;
B、由A得分析可知:随着F1的减小,刚开始时AB在两个力的作用下做加速度越来越小的加速运动,故B错误;
C、当F1单独在A上的加速度等于F2单独作用在B上的加速度时,AB之间恰好没有力的作用,此后F1继续减小,A的加速度继续减小,AB分离,根据牛顿第二定律得:F1=mAaB=8N,根据图象可知,此时t=12s,所以t=12?s时刻A、B将分离,分离时加速度均为a=2m/s2,故C正确;
D、AB分离前,A受到F1和B对A的弹力作用,分离后A只受F1作用,A物体加速度变化规律不相同,故D错误.
故选C
本题解析:
本题难度:简单
5、计算题 (10分)如图所示,AB是一段位于竖直平面内的弧形轨道,高度为h,末端B处的切线沿水平方向。一个质量为m的小物体P(可视为质点)从轨道顶端处A点由静止释放,滑到B点时以水平速度v飞出,落在水平地面的C点,其轨迹如图中虚线BC所示。已知P落地时相对于B点的水平位移OC=l,重力加速度为g,不计空气阻力的作用。

(1)请计算P在弧形轨道上滑行的过程中克服摩擦力所做的功;
(2)现于轨道下方紧贴B点安装一水平传送带,传送带右端E轮正上方与B点相距。先将驱动轮锁定,传送带处于静止状态。使P仍从A点处由静止释放,它离开B点后先在传送带上滑行,然后从传送带右端水平飞出,恰好仍落在地面上C点,其轨迹如图中虚线EC所示。若将驱动轮的锁定解除,并使驱动轮以角速度ω顺时针匀速转动,再使P仍从A点处由静止释放,最后P的落地点是D点(图中未画出)。已知驱动轮的半径为r,传送带与驱动轮之间不打滑,且传送带的厚度忽略不计。求:
①小物块P与传送带之间的动摩擦因数;
②若驱动轮以不同的角速度匀速转动,可得到与角速度ω对应的OD值,讨论OD的可能值与ω的对应关系。
参考答案:(1)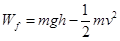 ;
;
(2)①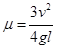 ;
;
②当0﹤ω﹤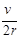 时,OD=l;当ω﹥
时,OD=l;当ω﹥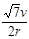 时,OD=(
时,OD=(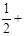
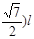 ;当
;当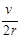 ﹤ω﹤
﹤ω﹤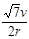 时,OD=
时,OD=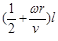 。
。
本题解析:(1)小物块从A到B的过程中有重力和摩擦力对其做功,
故根据动能定理有: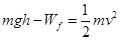 (2分)
(2分)
解得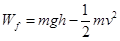 (1分)
(1分)
(2)① 需要先求出物块在E点的速度;
没有安装传送带时,小物块从B到C的过程,做平抛运动,水平方向有l=vt;
安装传送带后,小物块从E到C的过程沿水平方向有l/2=vEt,二者的竖直高度相等,落下时所用的时间相等,故联立以上两个方程,解得vE=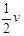 (1分)
(1分)
设小物块与传送带之间的动摩擦因数为μ,小物块从B到E的过程,根据动能定理有
-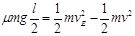 ?(2分)?
?(2分)?
解得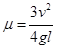 (1分)
(1分)
②(a)当传送带的速度0﹤v带=ωr﹤vE,
即0﹤ω﹤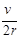 时,物体在传送带上一直做匀减速运动,物体离开传送带时的速度为vE,则OD=l…(1分)
时,物体在传送带上一直做匀减速运动,物体离开传送带时的速度为vE,则OD=l…(1分)
(b)如果传送带的速度较快,物体在传送带上一直加速而未与传送带共速,则物体的加速度始终为a=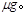 设物体离开传送带时的速度为vmax,
设物体离开传送带时的速度为vmax,
根据运动学公式有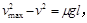 解得vmax=
解得vmax=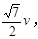
当传送带的速度v带=ωr﹥ ,
,
即ω﹥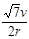 时,物体离开传送带点时的速度为vmax,
时,物体离开传送带点时的速度为vmax,
则OD=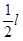 +
+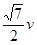 t=(
t=(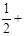
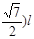 …(1分)
…(1分)
(c)当传送带的速度vE﹤v带=ωr﹤vmax,
即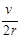 ﹤ω﹤
﹤ω﹤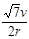 时,物体离开传送带点时的速度为v带=ωr,则OD=
时,物体离开传送带点时的速度为v带=ωr,则OD=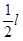 +ωrt=
+ωrt=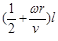 …(1分)
…(1分)
本题难度:一般