1、计算题  （10分）一个质量为m的小球拴在钢绳的一端，另一端施加大小为F1的拉力作用，在水平面上做半径为R1的匀速圆周运动。今将力的大小改变为F2，使小球仍在水平面上做匀速圆周运动，但半径变为R2，小球运动的半径由R1变为R2过程中拉力对小球做的功。

参考答案：

本题解析：设半径为R1、R2时小球的线速度大小分别为，由向心力公式可知：

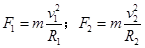
由动能定理得：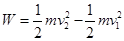
联立解得：

本题难度：一般

2、选择题  如图所示，AB是某电场中的一条电场线。若有一电子以某一初速度，仅在电场力的作用下，沿AB由A运动到B，其速度图象如下图所示，下列关于A、B两点的电场强度EA、EB和电势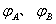的判断正确的是：

[? ]
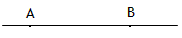
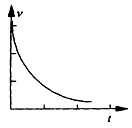
A．EA>EB
B．EA<EB
C．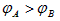
D．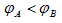

参考答案：AC

本题解析：

本题难度：一般

3、计算题  (8分)如图，光滑水平面AB与竖直面的半圆形导轨在B点相连接，导轨半径为R，一质量为m的静止木块在A处压缩弹簧，释放后，木块获得一向右的初速度，当它经过B点进入导轨瞬间对导轨的压力是其重力的7倍，之后向上运动恰能通过轨道顶点C，不计空气阻力，试求：

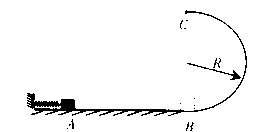
(1)弹簧对木块所做的功；
(2)木块从B到C过程中克服摩擦力做的功；

参考答案：⑴、⑵、

本题解析：本题考查对动能定理的应用，弹簧对物块做功转化为物体的动能，在B点根据合力提供向心力可求出B点动能，即可求出弹簧对木块做功，在C点只有重力提供向心力，可求出C点动能，从B点到C点应用动能定理可求得第二问

本题难度：一般

4、计算题  （20分）如图所示为一种获得高能粒子的装置。环形区域内存在垂直纸面向外、大小可调的匀强磁场。M、N为两块中心开有小孔的极板，每当带电粒子经过M、N板时，都会被加速，加速电压均为U；每当粒子飞离电场后，M、N板间的电势差立即变为零。粒子在电场中一次次被加速，动能不断增大，而绕行半径R不变（M、N两极板间的距离远小于R）。当t=0时，质量为m、电荷量为+q的粒子静止在M板小孔处。

（1）求粒子绕行n圈回到M板时的动能En；
（2）为使粒子始终保持在圆轨道上运动，磁场必须周期性递增，求粒子绕行第n圈时磁感应强度B的大小；
（3）求粒子绕行n圈所需总时间tn。

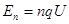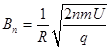参考答案：（1）?（2）（3）

本题解析：（1）粒子绕行一圈动能的增量为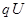，绕行n圈所获得的总动能（5分）
（2）因为 ?洛伦兹力提供向心力?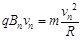
可得?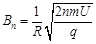?（6分）
（3）粒子做半径为R的匀速圆周运动，每一圈所用时间为，由于每一圈速度不同，所以每一圈所需时间也不同
第一圈： ?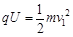
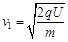
第二圈： ?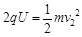
……
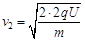
第n圈的速度?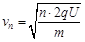?（4分）
故绕行n圈所需总时间
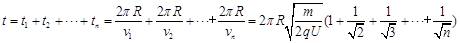?（5分）

本题难度：一般

5、选择题  质量分别为m和2m的小球a和b之间用一根轻质细杆连接，两小球可绕过细杆中心的水平轴无摩擦的转动，现让细杆水平，由静止释放后，在转动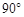的过程中，以下说法正确的是（?）

A．a的机械能守恒
B．b的机械能守恒
C．杆对a的弹力沿杆的方向，不对a做功
D．a、b系统机械能守恒

参考答案：D

本题解析：由于在整个的过程中，如果我们把小球a、b看成一个整体，则它们只受重力的作用，故机械能守恒，D是正确的；再单独对小球a而言，它在上升，并运动越来越快，故机械能增加，不守恒，A不对；虽然小球b下降，速度增加，但由于杆对小球b有弹力，故重力与弹力的功之和才等于b的动能增加量，故b的机械能也不守恒，B不对；杆对a的弹力并不沿杆的方向，而是向上，这样由于弹力对a的功大于重力对它的功，故其机械能增加，如果弹力沿杆的方向，球a是不会上升的，故C也不对，所以该题选D。

本题难度：一般