1、选择题  关于机械能守恒定律的适用条件，下列说法中正确的是
[? ]
A.只有重力和弹性力作用时，机械能守恒
B.当有其他外力作用时，只要合外力为零，机械能守恒
C.当有其他外力作用时，只要其他外力的合外力做功为零，机械能守恒
D.炮弹在空中飞行不计阻力时，仅受重力作用，所以爆炸前后机械能守恒

参考答案：C

本题解析：

本题难度：简单

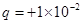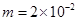2、计算题  如图所示，两平行金属板A、B水平放置，两板间的距离d=40cm．电源电动势E=24V，内电阻r=1Ω，电阻R=15Ω．闭合开关S，待电路稳定后，在两板之间形成匀强电场．在A板上有一个小孔k，一个带电荷量为C、质量为kg的粒子P由A板上方高h=10cm处的O点自由下落，从k孔进入电场并打在B板上点处．当P粒子进入电场时，另一个与P相同的粒子Q恰好从两板正中央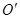点水平飞入．那么，滑动变阻器接入电路的阻值为多大时，粒子Q与P恰好同时打在处。 （粒子间的作用力及空气阻力均忽略不计，取g=10m/s2）

参考答案：滑动变阻器接入电路的阻值为8Ω

本题解析：
试题分析:根据机械能守恒定律可得P粒子进入电场时的速度为：
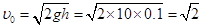m/s
设P、Q在电场中运动的加速度为a，运动到打在点的时间为t，则：
对P：?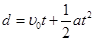
对Q：
联立解得：s，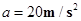
而
所以，滑动变阻器两端的电压为：

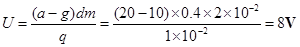
由欧姆定律可得通过滑动变阻器的电流为：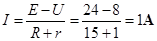
所以，滑动变阻器接入电路的阻值为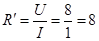：Ω

本题难度：一般

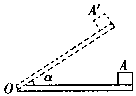
3、选择题  如图所示，木板OA水平放置，长为L，在A处放置一个质量为m的物体，现绕O点缓慢抬高到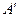端，直到当木板转到与水平面成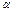角时停止转动.这时物体受到一个微小的干扰便开始缓慢匀速下滑，物体又回到O点，在整个过程中（?）
?
①持力对物体做的总功为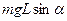
②摩擦力对物体做的总功为零
③木板对物体做的总功为零
④木板对物体做的总功为正功
A．①②
B．②③
C．①④
D．①③

参考答案：D

本题解析：物体从A点到A/的过程中，只有重力G和支持力N做功，由动能定理?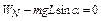，在此过程中支持力做功为，从A/回到O点的过程中支?持力的方向与路径始终垂直，所以支持力不做功，①正确.重力做的总功为零，支持力做?的总功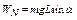，由动能定理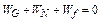得得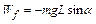，②不正确.木板对?物体的作用力为支持力N和摩擦力F，由得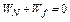即木板对物体做?的功为零，③正确，④错误.

本题难度：简单

4、计算题  （文）如图所示的半圆形光滑轨道，半径为R，固定于水平面上，一质量为m的物体从A点静止下滑。求

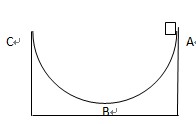
（1）物体滑到最低点B的速度为多大
（2）物体滑到最低点时对轨道的压力多大。

参考答案：（1）?（2）3mg

本题解析：（1）由于轨道是光滑的，所以机械能守恒，即
，化简则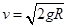
（2）在最低点根据向心力知识则：
将速度带入则F=3mg
点评：本题属于典型的圆周运动与机械能守恒定律的结合问题。在本题中机械能守恒定律求速度，通过圆周运动求出相应作用力

本题难度：简单

5、选择题  如图所示，质量为m的小球套在倾斜放置的固定光滑杆上，一根轻质弹簧的一端悬挂于O点，另一端与小球相连，弹簧与杆在同一竖直平面内，将小球沿杆拉到弹簧水平位置由静止释放，小球沿杆下滑，当弹簧位于竖直位置时，小球速度恰好为零，此时小球下降的竖直高度为h，若全过程中弹簧始终处于伸长状态且处于弹性限度范围内，下列说法正确的是(? )

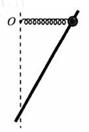
A．弹簧与杆垂直时，小球速度最大
B．弹簧与杆垂直时，小球的动能与重力势能之和最大
C．小球下滑至最低点的过程中，弹簧的弹性势能增加量小于mgh
D．小球下滑至最低点的过程中，弹簧的弹性势能增加量等于mgh

参考答案：BD

本题解析：光滑杆没有摩擦力做功，杆的弹力和运动方向垂直也不做功，那么整个过程只有弹簧弹力和小球重力做功，二者组成的系统机械能守恒，分析小球的受力，在沿杆方向一个是自身重力分力另外一个是弹力沿杆方向的分力，当弹簧与杆垂直时，沿杆方向没有弹簧的分力，只有重力沿杆向下的分力，说明小球在沿杆向下加速，所以速度不竖直最大答案A错。由于全过程弹簧始终处于伸长状态那么弹簧与杆垂直时弹簧伸长量最小，弹性势能最小，根据小球弹簧系统机械能守恒，此时小球机械能最大，即动能和重力势能之和最大答案B对。从初位置到末位置，小球速度都是0动能不变，重力势能减速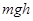，根据系统机械能守恒，弹簧弹性势能增加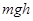答案D对C错。

本题难度：一般