1、选择题  物体在水平恒力作用下，在水平面上由静止开始运动．当位移s时撤去F，物体继续前进3s后停止运动，若路面情况相同，则物体的摩擦力和最大动能是（　　）
A．f=

参考答案：在物体的整个运动过程中，由动能定理得：
Fs-f（s+3s）=0-0
解得：f=F4；
从物体开始运动到撤去外力的过程中，由动能定理得：
Fs-fs=Ekm-0
解得：Ekm=3Fs4；所以选项D正确，ABC错误．
故选：D．

本题解析：

本题难度：一般

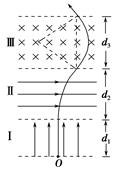
2、计算题  如图所示空间分为Ⅰ，Ⅱ，Ⅲ三个足够长的区域，各边界面相互平行，其中Ⅰ，Ⅱ区域存在匀强电场EI＝1.0×104 V/m，方向垂直边界面竖直向上；EⅡ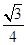＝×105 V/m，方向水平向右，Ⅲ区域磁感应强度B＝5.0 T，方向垂直纸面向里，三个区域宽度分别为d1＝5.0 m，d2＝4.0 m，d3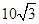＝?m．一质量m＝1.0×10－8 kg、电荷量q＝1.6×10－6C的粒子从O点由静止释放，粒子重力忽略不计．求：

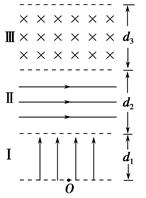
(1)粒子离开区域Ⅰ时的速度大小；
(2)粒子从区域Ⅱ进入区域Ⅲ时的速度方向与边界面的夹角；
(3)粒子从O点开始到离开Ⅲ区域时所用的时间．

参考答案：(1) v1＝4×103 m/s? (2) θ＝30°? (3)6.12×10-3s

本题解析：(1)由动能定理得 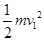＝qEId1?①?（2分）
得：v1＝4×103 m/s? ②?（1分）
(2)粒子在区域Ⅱ做类平抛运动．水平向右为y轴，竖直向上为x轴．设粒子进入区域Ⅲ时速度与边界的夹角为θ

tan θ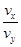＝? ③（1分）
vx＝v1　? vy＝at? ④（1分）
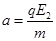? ⑤（1分）
t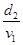＝? ⑥（1分）
把数值代入得θ＝30°⑦（1分）
(3)粒子进入磁场时的速度v2＝2v1?⑧（1分）
粒子在磁场中运动的半径R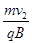＝＝10m?⑨（1分）
粒子在磁场中运动所对的圆心角为120°?因此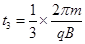（1分）
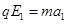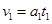?（两式共1分）
由（2）得
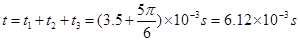（1+1=2分）

本题难度：一般

3、简答题  
（1）用水平拉力将小球从平衡位置P点很缓慢地移动到Q点，此时轻绳与竖直方向的夹角为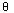，求拉力做的功。
（2）在Q点撤去拉力，让小球从静止开始下摆，求小球经过P点时的速度。

参考答案：（1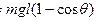）?（2）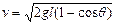

本题解析：（1）小球缓慢移动，动能不变。由动能定理
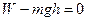?（5分）
解得拉力做的功为?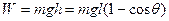?（3分）
（2）撤去拉力后，设小球经过P点时的速度为v，根据动能定理，重力做的功等于小球增加的动能，即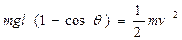?（5分）
解得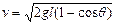

本题难度：简单

4、填空题  如图所示，在水平向左的匀强电场中，一根不可伸长的绝缘细线长度为L，一端拴一个质量为m电荷量为q的带负电小球，另一端固定在O点．把小球拉到使细线水平伸直的位置A然后将小球由静止释放，小球沿弧线运动到细线与水平方向成θ=60°的位置B时速度为零．则电场强度E=______，小球运动过程中的最大速率为______．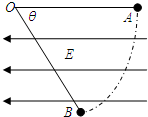

参考答案：由动能定理可知：
mgLsin60°-EqL（1-cos60°）=0
解得：E=

本题解析：

本题难度：一般

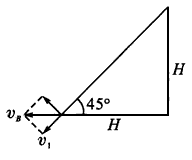
5、计算题  如图所示，一辆车通过一根跨过定滑轮的绳提升某质量为m的物体，绳不可伸长，绳的质量、定滑轮的质量及大小不计，滑轮的摩擦不计，开始时车在A点，绳已绷紧，与车相连的一段绳处于竖直方向上，绳与车的连接点到定滑轮的距离为H车从A点起向左加速运动到B点，通过的位移为H，车通过B点时速度为vB，求此过程中绳Q端对物体所做的功．

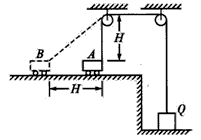
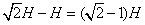参考答案：解：如图所示，车到B点时，物体上升的速度等于vB沿绳方向的分速度。车由A到B过程中绳被拉过，所以物体上升高度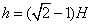，此过程中重力做功。由动能定理得W+ 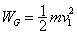，所以绳的拉力做功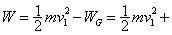

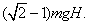
本题解析：

本题难度：困难