1、简答题  如图所示为研究电子枪中电子在电场中运动的简化模型示意图．在Oxy平面的ABCD区域内，存在两个大小均为E的匀强电场I和II，两电场的边界均是边长为L的正方形（不计粒子所受重力）．
（1）在该区域AB边的中点处由静止释放电子，求电子离开ABCD区域的位置；
（2）在电场I区域内适当位置由静止释放电子，电子恰能从ABCD区域左下角D处离开，求所有释放点的位置；
（3）若将左侧电场II整体水平向右移动L/4，仍使电子从ABCD区域左下角D处离开（D不随电场移动），在电场I区域内由静止释放电子的所有位置．

参考答案：（1）设电子的质量为m，电量为e，在电场I中释放后将做出速度为零的匀加速直线运动，出区域I时的速度为vo，接着进入电场II做类平抛运动，假设电子从CD边射出，出射点纵坐标为y，对电子的整个运动过程运用动能定理和匀变速直线运动公式有：eEL=12mv2，
在电场Ⅱ区域内的偏转，L=vt，y1=12at2=eE2m?L2v2=14L，方向向下，
故：y=L2-y1=L4
所以位置坐标（-2L，14L）
（2）设释放位置坐标为（x，y），在电场I中电子被加速到v1，然后进入电场II做类平抛运动，并从D点离开，有：eEx=12mv2，
L=vt，y?=12at2=eE2m?L2v2=L24x，所以满足xy=L24方程的点即为释放点的位置
（3）设释放位置坐标为（x，y），eEx=12mv2，在电场I中加速到v2，进入电场II后做类平抛运动，在高度为y′处离开电场II时的情景与（2）中类似，然后电子做匀速直线运动，经过D点，则有：
L=vt1，L4=vt2，
y2=12at21=eE2m?L2v2=L24x，
y3=at1t2=eEm?Lv?L4v=eEL24mv2=L28x，
y=y2+y3=L24x+L28x=3L28x，
所以满足y=3L28x方程的点即为释放点的位置．
答：（1）在该区域AB边的中点处由静止释放电子，电子从（-2L，14L）离开ABCD区域．
（2）在电场I区域内适当位置由静止释放电子，电子恰能从ABCD区域左下角D处离开，所有释放点为满足xy=L24的位置．
（3）若将左侧电场II整体水平向右移动在电场I区域内由静止释放电子的所有位置，在电场I区域内由静止释放电子的所有位置为y=3L28x．

本题解析：

本题难度：一般

2、简答题  如图所示，光滑绝缘水平面AB与倾角θ=370，长L=6m的绝缘斜面BC在B处圆滑相连，在斜面的C处有一与斜面垂直的弹性绝缘挡板，质量m=0.5kg、所带电荷量q=5x10-5C的绝缘带电滑块置于斜面的中点D，整个空间存在水平向右的匀强电场，场强E=2xlO5N/C，现让滑块以v0=12m/s的速度沿斜面向上运动．设滑块与挡板碰撞前后所带电荷量不变、速度大小不变，滑块和斜面间的动摩擦因数μ=0.1，求：
（1）滑块第一次与挡板碰撞时的速度大小；
（2）滑块第一次与挡板碰撞后能达到左端的最远点离B点的距离；
（3）滑块运动的总路程．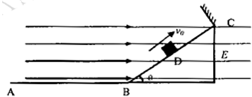

参考答案：（1）滑块从D到C的过程中，根据动能定理可得：
qEcosθ?L2-mgsinθ?L2-Ff?L2=12mv2C-12mv2D?
而滑动摩擦力：Ff=μ（mgcosθ+qEsinθ）?
解得vC=

本题解析：

本题难度：一般

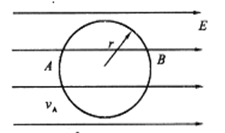
3、计算题  （10分）如图2所示，半径为r的绝缘细圆环的环面固定在水平面上，场强为E的匀强电场与环面平行。一电量为+q、质量为m的小球穿在环上，可沿环作无摩擦的圆周运动，若小球经A点时，速度vA的方向恰与电场垂直，且圆环与小球间沿水平方向无力的作用，试计算：

（1）小球运动达到最大速度的位置(半径与竖直方向成的角度θ用字母表示)
(2) 速度vA的大小；
（3）小球运动到与A点对称的B点时，对环在水平方向的作用力。

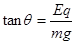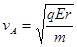参考答案：(1) （2）（3）。

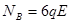本题解析：(1)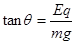
（2）在A点，小球在水平方向只受电场力作用，根据牛顿第二定律得：
?所以小球在A点的速度。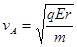
（3）在小球从A到B的过程中，根据动能定理，电场力做的正功等于小球动能的增加量，即?，
小球在B点时，根据牛顿第二定律，在水平方向有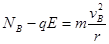
解以上两式，小球在B点对环的水平作用力为：。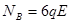
本题考查复合场和圆周运动、动能定理的综合应用，把重力和电场力进行合成，转化为等效重力场，在等效重力场的最低点小球速度最大，根据圆周运动沿着半径方向的合力提供向心力可求得在A点速度大小，从A到B运动过程中只有电场力做功，由动能定理求得B点速度，再由圆周运动的合力提供向心力求得环的支持力大小
点评：本题综合性比较强，考到的知识点很多，这就需要学生对圆周运动、动能定理、等效重力场的受力特点非常熟悉并能够加以应用

本题难度：一般

4、计算题  如图所示为某小区儿童娱乐的滑滑梯示意图，其中AB为斜面滑槽，与水平方向夹角为37o，BC为水平滑槽，与半径为0.2m的1／4圆弧CD相切，ED为地面.已知儿童在滑槽上滑动时的动摩擦系数都是0.5，A点离地面的竖直高度AE为2m，试求：
（1）儿童由A处静止起滑到B处时的速度大小
（2）为了使儿童在娱乐时不会从C处脱离圆弧水平飞出，水平滑槽BC长至少为多少? (B处的能量损失不计)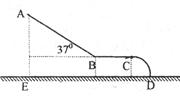

参考答案：（1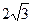）?m/s?（3分）
（2）1m? (5分)

本题解析：略

本题难度：简单

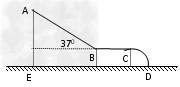
5、计算题  如图所示为儿童娱乐的滑梯示意图，其中AB为斜面滑槽，与水平方向夹角为37°，BC为水平滑槽，与半径为0.2m的1/4圆弧CD相切，ED为地面。已知通常儿童在滑槽上滑动时的动摩擦系数是0.5，A点离地面的竖直高度AE为2m，试求：(g取10m/s2)
(1)儿童在斜面滑槽上下滑时的加速度大小。
(2)儿童由A处静止起滑到B处时的速度大小。
(3)为了儿童在娱乐时不会从C处平抛射出，水平滑槽BC长至少为多少？

参考答案：解：（1）== =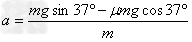
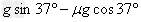（2）AF=AE-R=2m-0.2m=1.8m

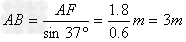
儿童从A处到B处，由动能定理可得：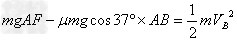
∴
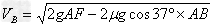
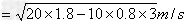
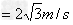
（3）若儿童恰好从C处平抛出，则儿童在C处时不受地面的弹力作用
即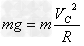
即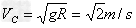
儿童从B到C处，由动能定理可得：
∴
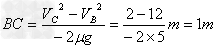
所以BC长至少为1m

本题解析：

本题难度：一般