1、计算题 1932年美国物理学家劳伦斯发明了回旋加速器,巧妙地利用带电粒子在磁场中的运动特点,解决了粒子的加速问题。现在回旋加速器被广泛应用于科学研究和医学设备中。
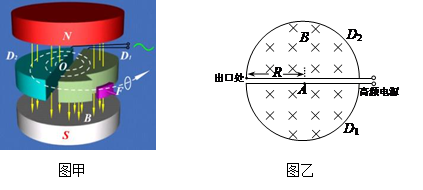
某型号的回旋加速器的工作原理如图甲所示,图乙为俯视图。回旋加速器的核心部分为D形盒,D形盒装在真空容器中,整个装置放在电磁铁两极之间的磁场中,磁场可以认为是匀强磁场,且与D形盒盒面垂直。两盒间狭缝很小,带电粒子穿过的时间可以忽略不计。质子从粒子源A处进入加速电场的初速度不计,从静止开始加速到出口处所需的时间为t。已知磁场的磁感应强度为B,质子质量为m、电荷量为+q,加速器接一定频率高频交流电源,其电压为U。不考虑相对论效应和重力作用。求:
(1)质子第1次经过狭缝被加速后进入D形盒运动轨道的半径r1;
(2)D形盒半径为R;
(3)试推理说明:质子在回旋加速器中运动时,随轨道半径r的增大,同一盒中相邻轨道半径之差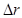 是增大、减小还是不变?
是增大、减小还是不变?
参考答案:(1) (2)
(2)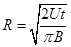 (3)减小.
(3)减小.
本题解析:(1) 设质子第1次经过狭缝被加速后的速度为v1
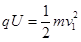 ①
①  ②
②
联立①②解得:
(2) 设质子从静止开始加速到出口处运动了n圈,质子在出口处的速度为v
 ③
③  ④
④
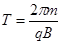 ⑤
⑤ 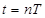 ⑥
⑥
联立③④⑤⑥解得 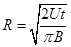
(3) (方法1)设k为同一盒子中质子运动轨道半径的序数,相邻的轨道半径分别为rk,rk+1(rk<rk+1),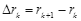 ,在相应轨道上质子对应的速度大小分别为vk,vk+1,D1、D2之间的电压为U,由动能定理知
,在相应轨道上质子对应的速度大小分别为vk,vk+1,D1、D2之间的电压为U,由动能定理知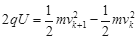 ⑦
⑦
由洛伦兹力充当质子做圆周运动的向心力,知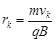 ,则
,则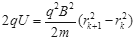 ⑧
⑧
整理得 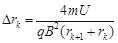 ⑨
⑨
相邻轨道半径rk+1,rk+2之差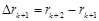 同理
同理 
因U、q、m、B均为定值,且因为rk+2> rk,比较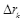 与
与 得
得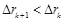
(方法2)设k为同一盒子中质子运动轨道半径的序数,相邻的轨道半径分别为rk-1、rk、rk+1,(rk-1<rk<rk+1),
由 及
及 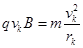 得
得
得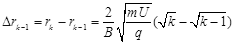
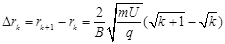
假设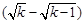 >
>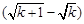 有
有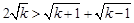
两边平方得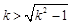 结果正确,说明假设成立。
结果正确,说明假设成立。
所以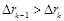
考点:回旋加速器;带电粒子在匀强电场及匀强磁场中的运动。
本题难度:一般
2、简答题 图为测量某种离子的比荷的装置.让中性气体分子进入电离室A,在那里被电离成离子.这些离子从电离室的小孔飘出,从缝S1进入加速电场被加速,然后让离子从缝S2垂直进入匀强磁场,最后打在底片上的P点.已知加速电压为U,磁场的磁感应强度为B,缝S2与P之间的距离为a,离子从缝S1进入电场时的速度不计,求该离子的比荷
.

参考答案:离子在电场中加速,根据动能定理得,
qU=12mv2.
离子在磁场中偏转,有:qvB=mv2r
又r=a2
联立以上各式解得qm=8UB2a2.
答:该离子的比荷qm=8UB2a2.
本题解析:
本题难度:一般
3、简答题 如图所示,在xoy平面内有很多质量为m、电量为e的电子,从坐标原点O不断以相同的速率V0沿不同方向平行xoy平面射入第I象限。现加一垂直xoy平面向里、磁感强度为B的匀强磁场,要求这些入射电子穿过磁场都能平行于x轴且沿X轴正方向运动。求符合条件的磁场的最小面积。(不考虑电子之间的相互作用)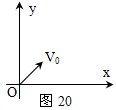
参考答案: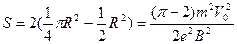
本题解析:如图21所示,电子在磁场中做匀速圆周运动,半径为 。在由O点射入第I象限的所有电子中,沿y轴正方向射出的电子转过1/4圆周,速度变为沿x轴正方向,这条轨迹为磁场区域的上边界。下面确定磁场区域的下边界。
。在由O点射入第I象限的所有电子中,沿y轴正方向射出的电子转过1/4圆周,速度变为沿x轴正方向,这条轨迹为磁场区域的上边界。下面确定磁场区域的下边界。
设某电子做匀速圆周运动的圆心O/与O点的连线与y轴正方向夹角为θ,若离开磁场时电子速度变为沿x轴正方向,其射出点(也就是轨迹与磁场边界的交点)的坐标为(x,y)。由图中几何关系可得
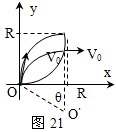
x=Rsinθ,y=R-Rcosθ,
消去参数θ可知磁场区域的下边界满足的方程为x2+(R-y)2=R2,(x>0,y>0)
这是一个圆的方程,圆心在(0,R)处。磁场区域为图中两条圆弧所围成的面积。磁场的最小面积为;
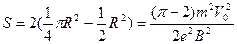
本题难度:简单
4、选择题 一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16( )
A.该原子核发生了α衰变
B.反冲核沿小圆做逆时针方向运动
C.原静止的原子核的原子序数为15
D.沿大圆和沿小圆运动的粒子的周期相同