1、选择题 在匀强磁场中,把一个重力不计的带电粒子由静止释放,这个带电粒子可能
[? ]
A.做匀速圆周运动
B.做匀加速直线运动
C.做匀速直线运动
D.保持静止状态
参考答案:D
本题解析:
本题难度:简单
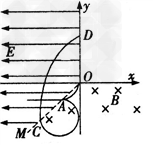
2、计算题 如图所示,在xOy平面内,第Ⅲ象限内的直线OM是电场与磁场的边界,OM与负x轴成45°角。在x<0且OM的左侧空间存在着沿x轴负方向的匀强电场E,场强大小为3.2N/C;在y<0且OM的右侧空间存在着垂直纸面向里的匀强磁场B,磁感应强度大小为0.01T。一不计重力的带负电的微粒,t=0时刻从坐标原点O沿y轴负方向以v0=2×103m/s的初速度进入磁场,最终离开电磁场区域。已知微粒的电荷量q=-5×10-8C,质量m=1×10-14kg,求:?
(1)带电微粒第一次经过磁场边界的位置坐标;?
(2)带电微粒在磁场区域运动的总时间;?
(3)带电微粒最终离开电、磁场区域的位置坐标。

参考答案:解:(1)带电微粒从O点射入磁场,运动轨迹如图所示,第一次经过磁场边界上的A点,由洛伦兹力公式和牛顿第二定律得:
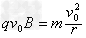
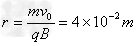
A点位置坐标为(-4×10-2 m,-4×10-2 m)
(2)设带电微粒在磁场中做圆周运动的周期为
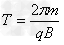
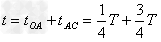
代入数据解得t=T=1.26×10-4 s
(3)微粒从C点沿y轴正方向进入电场,做类平抛运动
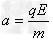
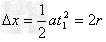
△y=v0t1
代入数据解得△y=0.2 m
y=△y-2r=(0.2-0.08)m=0.12 m
故离开电、磁场时的位置坐标为(0,0.12 m)
本题解析:
本题难度:困难
3、简答题

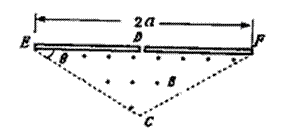
(1)若粒子恰好垂直于EC边射出磁场,求磁场的磁感应强度B为多少?
(2)改变磁感应强度的大小,粒子进入磁场偏转后能打到ED板,求粒子从进入磁场到第一次打到ED板的最长时间是多少?
(3)改变磁感应强度的大小,可以再延长粒子在磁场中的运动时间,求粒子在磁场中运动的极限时间。(不计粒子与ED板碰撞的作用时间。设粒子与ED板碰撞前后,电量保持不变并以相同的速率反弹)
参考答案:
(1)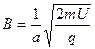 (2)
(2)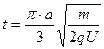 (3)
(3)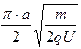
本题解析:(1)依题意,粒子经电场加速射入磁场时的速度为v
由 ?(2分)
?(2分)
得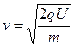 ?………………①
?………………①
粒子在磁场中做匀速圆周运动其圆心在E点,如图所示,半径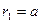 ?…………②
?…………②

本题难度:一般
4、计算题 如图所示,水平面xx´上竖直放着两根两平行金属板M、N,板间距离为L=1m,两板间接一阻值为2Ω的电阻,在N板上开一小孔Q,在M、N及Q上方有向里匀强磁场B0=1T;在Nx´范围内有一450分界线连接Q和水平面,NQ与分界线间有向外的磁感应强度B=0.5T的匀强磁场;N、水平面及分界线间有竖直向上的电场;现有一质量为0.2
参考答案:
本题解析:
本题难度:困难
5、计算题 A、B为一平行板,板长为l,两板间距离为d,板间区域内充满着匀强磁场,磁感应强度大小为B,方向垂直纸面向里。一个质量为m,带电荷量为+q的带电粒子以一定初速度沿A、B两板中线且垂直于磁感线方向射入磁场中,粒子恰好从A板的右边界飞出。粒子重力不计。求:
(1)粒子在磁场中运动的轨道半径r和射入磁场的初速度v0各是多少?
(2)粒子在磁场中运动的时间t是多少?
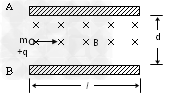
参考答案:解:(1)设粒子做圆周运动的圆心为O(如图)
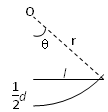
由几何条件可知:r2=l2+(r-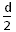 )2?①
)2?①
解之得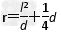
由牛顿第二定律可得:qv0B=m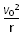 ?②
?②
解①、②式得v0=
(2)设粒子从磁场飞出时,转过的圆心角为θ,粒子做圆周运动的周期为T,则有
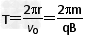 ?③
?③
tgθ=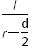 ?④
?④
t=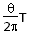 ?⑤
?⑤
解①、③、④、⑤得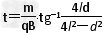 或
或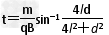
本题解析:
本题难度:一般