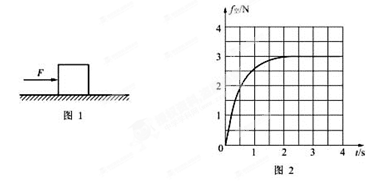
1、计算题  如图1所示，质量m=1.0kg的物块，在水平向右、大小F = 5.0N的恒力作用下，沿足够长的粗糙水平面由静止开始运动。在运动过程中，空气对物块的阻力沿水平方向向左，其大小f空=kv，k为比例系数，f空随时间t变化的关系如图2所示。g取10m/s2。

（1）求物块与水平面间的动摩擦因数μ；
（2）估算物块运动的最大速度vm；
（3）估算比例系数k。

参考答案：（1）?（2）?（3）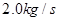

本题解析：（1）由图2可知，2s后空气对物块的阻力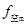大小不变，即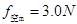，物块做匀速直线运动，设水平面对物块的摩擦力为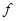，由平衡条件得：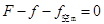
又因为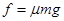　　
联立解得：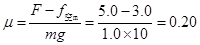
（2）因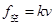随速度的增大而增大，而恒力F和水平面对物块的摩擦力为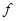保持不变，所以在内，物块做加速度逐渐减小的加速运动，匀速运动时速度达到最大，根据动量定理有

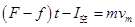
在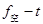图象中，图线与横轴围成的“面积”表示冲量，设每个小正方形的面积为，由图2可知，在内，图线与横轴围成的的“面积”内含有小正方形的个数为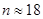，则

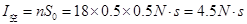
所以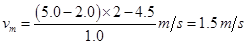　
（3）因为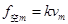，所以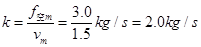

本题难度：一般

2、选择题  质量为60kg的人站在升降机内的台秤上，现测得其体重为880N，试确定升降机的运动情况（　　）
A．加速下降
B．加速上升
C．减速上升
D．无法确定

参考答案：根据题意可知人所受支持力大于自身重力，处于超重状态，人具有竖直向上的加速度，因此升降机的可能运动情况是加速上升或者减速下降，故ABC错误，D正确．
故选D．

本题解析：

本题难度：一般

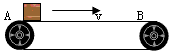
3、计算题  如图所示，水平传输带以4m/s的速度匀速运动，传输带两端A、B间的距离为20m，将一质量为2kg的木块无初速地放在A端，木块与传输带间的动摩擦因数为μ=0.2。试求：木块从A端运动到B端所用的时间？

参考答案：解：a=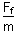=μg=2 m/s2
v=at1
t1=2 s
x1=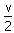t1=4 m
x2=L－x1=16 m
t2=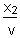=4 s
t=t1+t2=6 s

本题解析：

本题难度：一般

4、计算题  （10分）一质量为m ="40" kg的小孩站在电梯内的体重计上.电梯从t =0时刻由静止开始上升,在0到6 s内体重计示数F的变化如图所示.试问：在这段时间内电梯上升的高度是多少？取重力加速度g="10" m/s2.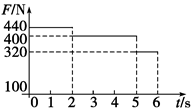

参考答案：9（m）

本题解析：选取小孩为研究对象，地面为参考系，小孩受到重力和体重计对小孩的弹力，如图所示.小孩的运动分为三个阶段.在0~2s内以加速度a1向上做匀加速直线运动，根据牛顿第二定律可得，加速度

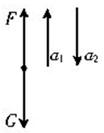
a1=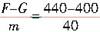=1（m/s2）
根据匀变速直线运动公式可得，第一阶段位移s1=1/2a1t12=1/2×1×22=2（m）
第一阶段末速度
v1=a1t1=1×2=2（m/s）
2s~5s内向上以速度v1做匀速直线运动，根据匀速直线运动公式可得，第二阶段位移?
s2=v1t2=2×3=6（m）
在5s~6s内以加速度a2向上做匀减速直线运动，根据牛顿第二定律可得，加速度
a2==2（m/s2）
设从速度v1减速为0的时间为t3，根据匀变速直线运动公式可得t3=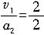=1（s）
则可判断小孩子在第6s末速度为0，第三阶段位移
s3=v1t3-1/2a2t32=2×1-1/2×2×12=1（m）
则在这段时间内小孩上升的高度，即电梯上升的高度
s=s1+s2+s3=2+6+1=9（m）
点评：难度中等，本题为多过程问题，注意把整个过程分解为独立分析的分过程，联系分过程的桥梁就是速度，结合牛顿第二定律和运动学公式求解

本题难度：一般

5、简答题  如图所示，商场工作人员用与水平方向成37°斜向上、大小为200N的力F拉着货物沿水平地面做匀速运动，货物的质量为52kg，速度大小为8m/s，某时刻撤去拉力后，货物滑行了一段距离停下（cos37°=0.8，sin37°=0.6）．求：
（1）货物与水平面间动摩擦因数多大？
（2）撤去拉力后，货物还能运动多长时间？
（3）若将力F改为水平，使此货物从静止开始运动，则F至少做多少功，能使货物到达200m处的仓库．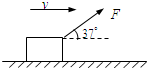

参考答案：（1）货物受重力、支持力、拉力摩擦力处于平衡，有：
Fcos37°=f
f=μ（mg-Fsin37°）
联立两式解得：μ=0.4．
（2）撤去拉力后，货物的加速度a=μmgm=μg=4m/s2
则货物还能运动的时间t=va=2s．
（3）根据动能定理得：
WF-μmgx=0
解得WF=μmgx=0.4×520×200J=4.16×104J．
答：（1）货物与水平面间动摩擦因数为0.4．
（2）撤去拉力后，货物还能运动2s．
（3）F至少做4.16×104J功，能使货物到达200m处的仓库．

本题解析：

本题难度：一般