1、选择题  关于重力和万有引力的关系，下列说法错误的是（　　）
A．地面附近物体所受到重力就是万有引力
B．重力是由于地面附近的物体受到地球吸引而产生的
C．在不太精确的计算中，可以近似认为其重力等于万有引力
D．严格说来重力并不等于万有引力，除两极处物体的重力等于万有引力外，在地球其他各处的重力都略小于万有引力

参考答案：A

本题解析：万有引力是由于物体具有质量而在物体之间产生的一种相互作用．任何两个物体之间都存在这种吸引作用．物体之间的这种吸引作用普遍存在于宇宙万物之间，称为万有引力．重力，就是由于地面附近的物体受到地球的万有引力而产生的，重力只是万有引力的一个分力． 故A错误．重力是由于地面附近的物体受到地球的吸引而产生的，故B正确．在不太精确的计算中，可以认为物体的重力等于万有引力，故C正确．严格来说重力并不等于万有引力，除两极处物体的重力等于万有引力外，在地球其他各处的重力都略小于万有引力，故D正确．
本题选错误的，故选A．
点评：物体由于地球的吸引而受到的力叫重力．知道重力只是万有引力的一个分力，忽略地球的自转，我们可以认为物体的重力等于万有引力．

本题难度：简单

2、选择题  据报道，最近在太阳系外发现了首颗“宜居”行星，其质量约为地球质量的6.4倍，一个在地球表面重量为600 N的人在这个行星表面的重量将变为960 N，由此可推知该行星的半径与地球半径之比约为

[? ]

参考答案：B

本题解析：

本题难度：一般

3、选择题  若已知月球绕地球运动可近似看做匀速圆周运动，并且已知月球绕地球运动的轨道半径r，它绕地球运动的周期T，万有引力常量是G，由此可以知道（　　）
A．月球的质量m=

参考答案：A、根据万有引力提供向心力，列出等式只能求出中心体的质量．故A错误．
B、研究月球绕地球做匀速圆周运动，根据万有引力提供向心力，列出等式GMmr2=m4π2rT2，可得太阳的质量M=4πr3GT2．故B正确；
C、D、不清楚月球和地球的半径大小，所以无法求出其密度，故C、D错误
故选B．

本题解析：

本题难度：简单

4、计算题  某行星探测器在其发动机牵引力作用下从所探测的行星表面竖直升空后，某时刻速度达到v0＝80m/s，此时发动机突然发生故障而关闭，已知该行星的半径为R＝5000km、第一宇宙速度是v＝5km/s。该行星表面没有大气，不考虑探测器总质量的变化及重力加速度随高度的变化。求：发动机关闭后探测器还能上升的最大高度。

参考答案：在该行星表面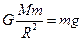?（4分）
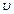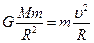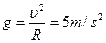设该行星的第一宇宙速度为，?（4分）
?（4分）
则探测器能上升的最大高度为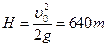?（4分）

本题解析：略

本题难度：一般

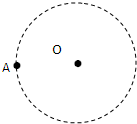
5、简答题  如图为宇宙中有一个恒星系的示意图．A为星系的一颗行星，它绕中央恒星O运行的轨道近似为圆．天文学家观测得到A行星运动的轨道半径为R0、周期为T0．
（1）中央恒星O的质量为多大？
（2）经长期观测发现，A行星实际运动的轨道与圆轨道总存在一些偏离，且周期性地每隔时间t0发生一次最大的偏离．天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知的行星B（假设其运行轨道与A在同一水平面内，且与A的绕行方向相同），它对A行星的万有引力引起A轨道的偏离（由于B对A的吸引而使A的周期引起的变化可以忽略）根据上述现象及假设，试求未知行星B的运动周期T及轨道半径R．

参考答案：（1）设中央恒星质量为M，A行星质量为m
由万有引力提供向心力得：GMmR20=m4π2R0T2
得：M=4π2R30GT20
（2）每隔时间t0发生一次最大的偏离，说明A、B每隔时间t0有一次相距最近的情况，这时它们转过的角度相差1周（2π），所以有：2πT0t0-2πTt0=2π
解得：T=t0T0t0-T0
据开普勒第三定律：R3T2=R30T20
得：R=(t0t0-T0)23R0
答：中央恒星O的质量为M=4π2R30GT20；未知行星B的运动周期T=t0T0t0-T0，及轨道半径R=(t0t0-T0)23R0．

本题解析：

本题难度：一般