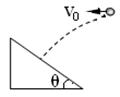
1、选择题  小球以水平初速v0抛出，飞行一段时间后，垂直撞在倾角为θ的斜面上，则可知小球的飞行时间是（?）

A．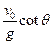
B．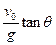
C．
D．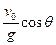

参考答案：A

本题解析：速度方向垂直斜面，则竖直方向的分速度与速度的夹角为θ，再利用三角函数求解

本题难度：一般

2、选择题  在高度为H的同一位置，向水平方向同时抛出两个小球A和B，如果vA＞vB，则下列说法中正确的是
[? ]
A．A球射程大于B球的射程
B．A球落地时间小于B球落地时间
C．如果两球在飞行中遇到一堵竖直的墙壁，两球击中墙的高度可能相同
D．在空中飞行的任意时刻，两球速率总是不同的

参考答案：AD

本题解析：

本题难度：简单

3、简答题  如图所示，网球运动员在网前做截击练习时，若练习者在球网正上方距地面高H处，将网球以一定的速度沿垂直球网的方向击出，已知底线到球网的水平距离为L，重力加速度为g，不计空气阻力，将球的运动视为平抛运动．
（1）求网球落地所用的时间；
（2）要使网球不出界，求运动员将球击出的最大速度．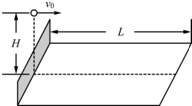

参考答案：（1）设网球落地所用的时间为t，则H=12gt2
所以t=

本题解析：

本题难度：一般

4、计算题  (12分) 如图所示，半径为R内径很小的光滑半圆管竖直放置，和水平面相切与B处，两个质量均为m的小球a、b以不同的速度进入管内，a通过最高点A时对管壁恰好没有作用力，b通过最高点A时，对管壁下部的压力为0.75mg，求：

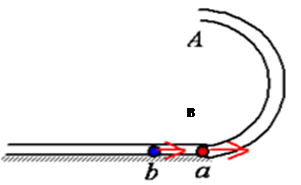
（1）a、b两球落地点间的距离
（2）a球在刚好进入管道B处时对管壁的压力大小

参考答案：（1）R（2）6mg

本题解析：以a球为对象，设其到达最高点时的速度为va，根据向心力公式有：
?
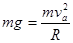所以： ?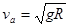
以b球为对象，设其到达最高点时的速度为vb，根据向心力公式有：
?
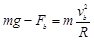即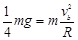?所以：?
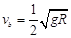a、b两球脱离轨道的最高点后均做一平抛运动，所以a、b两球的水平位移分别为：


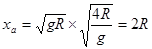
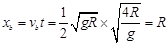
故a、b两球落地点间的距离?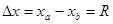
(2)对a球从B到A的过程中有
?
?　　　
?
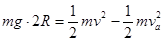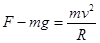点评：本题将物理学中常见的模型等巧妙结合，通过题目条件分析最高点速度即速度为零。利用向心力知识、匀变速直线运动规律等基础知识求解。

本题难度：一般

5、计算题  在倾角为37°的斜面上，从A点以6m/s的速度水平抛出一小球，小球落在B点，如图所示，求小球刚落到斜面时的速度方向，AB两点间距离和小球在空中飞行时间。（g=10m/s）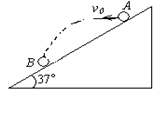

参考答案：arctan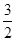

本题解析：小球落到B点时速度偏角为α，运动时间为t，则：
tan37°=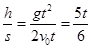?又因为tan37°=?
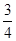解得t=0.9s? B两点间水平距离S=v0t=6×0.9m=5.4m
A．B两点间距离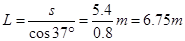
在B点时，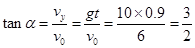
所以，小球捧到斜面时速度方向与水平方向间的夹角为arctan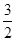
本题考查平抛运动规律的应用,小球落在斜面上根据位移与水平方向成37°角,把位移分解为水平分位移和竖直分位移,由竖直方向和水平方向的分运动列公式,由tan37°求解运动时间,再由分运动求得水平位移和竖直位移，由勾股定理求得合位移

本题难度：一般