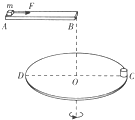
1、简答题 如图所示,水平放置的圆盘半径为R=1m,在其边缘C点固定一个高度不计的小桶,在圆盘直径CD的正上方放置一条水平滑道AB,滑道与CD平行.滑道右端B与圆盘圆心O在同一竖直线上,其高度差为h=1.25m.在滑道左端静止放置质量为m=0.4kg的物块(可视为质点),物体与滑道间的动摩擦因数为μ=0.2.当用一大小为F=4N的水平向右拉力拉动物块的同时,圆盘从图示位置以角速度ω=2πrad/s,绕穿过圆心O的竖直轴匀速转动,拉力作用一段时间后撤掉,物块在滑道上继续滑行,由B点水平抛出,恰好落入小桶内,重力加速度取10m/s2.
(1)物块离开B点水平抛出的初速度vB;
(2)分别求出拉力撤掉前后物块的加速度a1和a2;
(3)若拉力作用时间为0.5s,求所需滑道的长度L;
(4)调整拉力的作用时间和滑道的长度,物块仍恰好落入小桶内,求拉力作用的最短时间.
参考答案:(1)物块平抛:h=12gt2;
得:t=
本题解析:
本题难度:一般
2、计算题 (9 分)如图所示,光滑水平面上的O处有一质量为m=2Kg物体。物体受到两个水平力的作用,F1=4N,F2=(2+2x)N,x为物体相对O的位移。物体从静止开始运动,问:
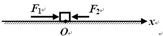
(1)当位移为x=0.5m时物体的加速度多大?
(2)在何位置物体的加速度最大?最大值为多少?
(3)在何位置物体的速度最大?最大值为多少?
参考答案:(1)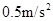 (2)
(2)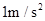 (3)1m/s
(3)1m/s
本题解析:
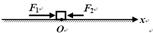
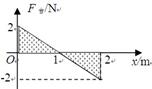
(1)当x=0.5m时,F2=(2+2×0.5)N=3N
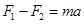
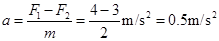 ?(2分)?
?(2分)?
(2)物体所受的合外力为

作出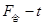 图如图所示:
图如图所示:
从图中可以看出,当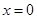 时,物体有最大加速度
时,物体有最大加速度 。
。
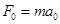
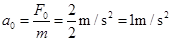
当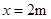 时,物体也有最大加速度
时,物体也有最大加速度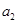 。
。
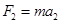
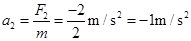
负号表示加速度方向向左。(4分)
(3)当物体的加速度为零时速度最大。从上述图中可以看出,当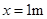 时,
时,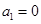 ,速度
,速度 最大。
最大。
从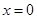 至
至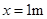 合外力所做的功为?
合外力所做的功为?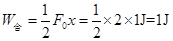
根据动能定理,有?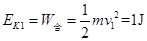
所以当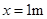 时,物体的速度最大,为
时,物体的速度最大,为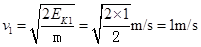 (3分)
(3分)
点评:牛顿第二定律连接了力和物体运动两个模块,加速度是关键
本题难度:一般
3、实验题 小明用电源频率为50Hz的电磁打点计时器(含复写纸)做“探究质量一定时,加速度与合力的关系”实验。

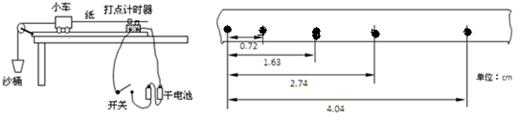
(1)在不挂配重,平衡摩擦力过程中,打点计时器打出的一条纸带如图(乙)所示,纸带A端与小车相连。要使小车做匀速直线运动,垫木应向____(填“左或右”)移动。
(2)打点计时器打A、C两点过程中,小车通过的距离为____cm。
(3)小王同学也做这个实验,他在接通电源进行实验之前,将实验器材组装如图丙所示.请你指出该装置中的错误或不妥之处(只要答出其中的两点即可):?
??。
丙?丁
(4)改正实验装置后,该同学顺利地完成了实验.图丁是他在实验中得到的一条纸带,图中相邻两计数点之间还有四个点没有画出来,由图中的数据可算得小车的加速度a为?m/s2.(结果取两位有效数字)
参考答案:1) 左? 2)16.20? 3)1。该同学用是直流电源? 2。木板的右端没有垫高 3)小车离打点计时器太远(每点2分,其他合理即可得分)? 4)0.20
本题解析:(1)平衡摩擦力后,小车做匀速直线运动,打出的纸带应是间距均匀的,由图可知,小车在做减速运动,所以,垫木应向左移动;(2)由图读得AC距离为16.20cm;(3)1.该同学用是直流电源,打点计时器使用的是交流电源? 2.木板的右端没有垫高,没有平衡摩擦力 3.小车离打点计时器太远,没充分利用好纸带;(4)用逐差法求纸带的加速度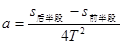 ,T=0.1s,代入数据可算得a=0.20m/s2。
,T=0.1s,代入数据可算得a=0.20m/s2。
本题难度:一般
4、选择题 关于汽车在水平路上运动,下列说法中正确的是( )
A.汽车以额定功率启动,在速度达到最大以前,加速度是在不断增大的
B.汽车以额定功率启动,在速率达到最大以前,牵引力应是不断减小的
C.汽车以恒定加速度启动,匀加速过程能达到的最大速度等于汽车最终的最大速度
D.汽车以恒定加速度启动,匀加速过程能达到的最大速度小于汽车最终的最大速度
参考答案:A、B汽车以额定功率启动时,由P=Fv可知,牵引力大小与速率成反比,则知汽车的速度逐渐增大,牵引力逐渐减小,合力减小,加速度减小,当牵引力大小与阻力大小相等时,汽车做匀速运动,速度达到最大.故在速率达到最大以前,牵引力应是不断减小的.故A错误,B正确.
C、D汽车以恒定加速度启动时,牵引力不变,随着速度增大,由P=Fv知,发动机的功率增大,当发动机的功率达到额定功率时,匀加速运动结束.由于此时牵引力大于阻力,汽车的速度继续增大,牵引力减小,加速度减小,当牵引力与阻力大小相等时,汽车做匀速运动,速度达到最大.可见,匀加速过程能达到的最大速度小于汽车最终的最大速度.故C错误,D正确.
故选BD
本题解析:
本题难度:一般
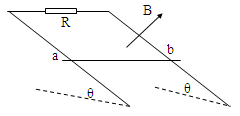
5、计算题 如图所示,两根相距L平行放置的光滑导电轨道,与水平面的夹角为θ,轨道间有电阻R,处于磁感应强度为B、方向垂直轨道向上的匀强磁场中,一根质量为m、电阻为r的金属杆ab,由静止开始沿导电轨道下滑,设下滑过程中杆ab始终与轨道保持垂直,且接触良好,导电轨道有足够的长度且电阻不计,求:
(1)金属杆的最大速度是多少;
(2)当金属杆的速度刚达到最大时,金属杆下滑的距离为S,求金属杆在此过程中克服安培力做的功;
(3)若开始时就给杆ab沿轨道向下的拉力F使其由静止开始向下做加速度为a的匀加速运动(a>gsinθ),求拉力F与时间t的关系式?
参考答案:(1)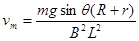 ;(2)
;(2)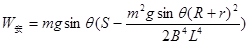
(3)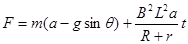
本题解析:(1)受力如图所示,当mgsinθ=F安时速度最大,设为vm
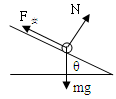
此时电动势: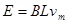 ,安培力:
,安培力:
由闭合电路欧姆定律:
得: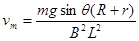
(2)由功能关系,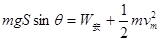
得: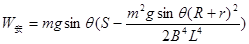
(3)经过时间t,杆的速度v=at
由牛顿第二定律:F+mgsinθ-BIL=ma
得: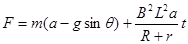
本题难度:一般