1、计算题  如图所示，一平直的传送带以v＝2 m/s的速度匀速运行，传送带把A处的工件运送到B处。A，B相距l＝10 m。从A处把工件无初速度地放到传送带上，经过时间t＝6 s传送到B处，欲用最短的时间把工件从A处传送到B处，求传送带的运行速度至少多大。

参考答案：解：工件从A处无初速度放在传送带上以后，将在摩擦力作用下做匀加速运动，因为，这表明工件从A到B先做匀加速运动，后做匀速运动。设工件做匀加速运动的加速度为a，加速的时间为t1，相对地面通过的位移为x，则有
v＝at1，x＝，x＋v(t－t1)＝l
数值代入得a＝1 m/s2
要使工件从A到B的时间最短，须使它始终做匀加速运动，至B点时速度为运送时间最短所对应的皮带运行的最小速度
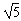由v2＝2al得v＝＝2 m/s

本题解析：

本题难度：一般

2、计算题  运动场上4×800m接力赛已进入了白热化阶段，甲、乙两队都已经是最后一棒。甲队员健步如飞，最大速度达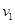=12m/s，乙队员也不甘落后奋力直追，可能是由于紧张，甲队员不小心将接力棒失落，回头拾起棒后，甲加速直追反超乙。现将甲的加速和减速过程都视为匀变速运动，且加速时的加速度大小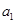=2m/s2,减速时的加速度大小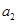=6m/s2，拾棒时的速度为零，不计棒脱手后的位移和拾棒动作所花的时间，问：（1）甲在返回拾棒过程中的最大速率为多少？
（2）甲因为拾棒而耽误了多少时间？
（3）若丢棒时甲领先乙△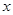=8m，而距离终点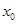=240m，乙的速度保持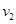=10m/s，通过计算分析甲能否赢得比赛？

参考答案：（1）6m/s（2）9s（3）甲能赢得比赛

本题解析：（1）丢棒后，甲先减速至零，其时间，
位移
之后反向加速，再减速至零，设最大速度为vm,则有: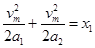,解得：vm=6m/s
(2)返回拾棒过程的时间为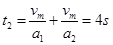
再继续加速前进到达最大速度的过程中，其时间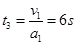
位移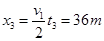
若是没丢棒，跑这段位移的时间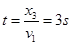
故耽误的时间为
(3) 从掉棒开始计时，甲到终点需要的时间= 29s
乙到终点需要的时间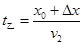=32s
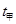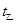＜，说明最终甲能赢得比赛。

本题难度：一般

3、计算题  在第21届温哥华冬奥会上，我国女子冰壶队取得了优异的成绩，比赛中，冰壶在水平冰面上的运动可视为匀减速直线运动，设一质量m=20kg的冰壶从被运动员推出到静止共用时t=20s，运动的位移x=30m，取g=10m/s2，求：冰壶在此过程中

（1）平均速度的大小；
（2）加速度的大小；
（3）所受平均阻力的大小。

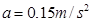参考答案：（1）?（2）（3）3N

本题解析：（1）根据平均速度公式：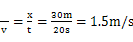
（2）根据匀变速直线运动公式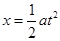：，即a=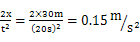
(3) 根据牛顿第二定律则F=ma，所以阻力大小为3N
点评：本题考查了牛顿第二定律的简单应用和计算。

本题难度：简单

4、填空题  物体从静止开始以2 m/s2的加速度做匀加速直线运动，则前6 s内的平均速度是______m／s。

参考答案：6

本题解析：

本题难度：一般

5、填空题  小木块沿光滑斜面下滑，初速度为零。当它滑过的距离为L时，速度大小为v。那么当它的速度为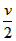时，滑过的距离是________。

参考答案：L/4

本题解析：

本题难度：一般