1、选择题  如图所示，一个质量为m的物体以某一速度从A点冲上倾角为30°的斜面，其运动的加速度大小为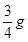，这物体在斜面上上升的最大高度为h，则在这一过程中（?）?
?
A．重力势能增加了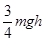
B．机械能损失了
C．动能损失了mgh
D．合外力对物体做功为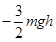

参考答案：BD

本题解析：由题意知，物体在斜面上上升的最大高度为h，克服重力做功为mgh，则重力势能增加了mgh．故A错误；根据牛顿第二定律得：mgsin30°+f=ma，得到摩擦力大小为f=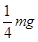，物体克服摩擦力做功为Wf=f?2h=，由功能关系知物体的机械能损失了，故B正确；合力对物体做功为W合=-ma?2h=-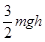，故D正确，又由动能定理得知，物体动能损失了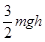，故C错误。

本题难度：一般

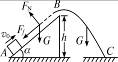
2、简答题  斜面AB与水平面夹角α=30°，B点距水平面的高度h="1" m,如图5-7-7所示.一个质量为m的物体，从斜面底端以初速度v0="10" m/s沿斜面向上射出，物体与斜面间的动摩擦因数μ=0.2,且物体脱离斜面以后的运动过程中空气阻力不计，求物体落到水平面时的速度vC.

图5-7-7

参考答案：9.65 m/s

本题解析：如图所示，物体落于C点时速度大小为vC，由动能定理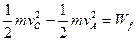：?①
而Wf=-μmgcos30°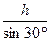?②
解①、②式及VA=V0得VC=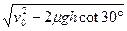="9.65" m/s

本题难度：简单

3、选择题  如图1所示，物体以一定初速度从倾角α=37°的斜面底端沿斜面向上运动，上升的最大高度为3.0m．选择地面为参考平面，上升过程中，物体的机械能E机随高度h的变化如图2所示．g=10m/s2，sin37°=0.60，cos37°=0.80．则（　　）

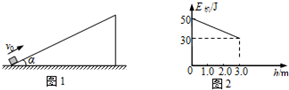
A．物体的质量m=0.67kg
B．物体与斜面间的动摩擦因数μ=0.40
C．物体上升过程的加速度大小a=10m/s2
D．物体回到斜面底端时的动能Ek=10J

参考答案：A、物体到达最高点时，机械能E=EP=mgh，m=Egh=3010×3=1kg，故A错误；
B、物体上升过程中，克服摩擦力做功，机械能减少，减少的机械能等于克服摩擦力的功，
△E=-μmgcosαhsinα，即30-50=-μ×1×10cos37°×3sin37°，μ=0.5，故B错误；
C、物体上升过程中，由牛顿第二定律得：mgsinα+μmgcosα=ma，解得a=10m/s2，故C正确；
D、由图象可知，物体上升过程中摩擦力做功W=30-50=-20J，在整个过程中由动能定理得EK-EK0=2W，
则EK=EK0+2W=50+2×（-20）=10J，故D正确；
故选CD．

本题解析：

本题难度：一般

4、选择题  如图所示，光滑水平面上，质量为m的小球A和质量为