1、简答题  如图是一个透明圆柱介质的横截面，B、C为圆上两点．一束单色光沿AB方向入射，从c点射出，已知∠ABO=∠BOC=120°，真空中光速c=3×108m/s．求：
①光在介质中的折射率n
②光在介质中传播速度v．

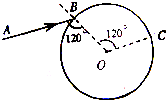
参考答案：①由题得，入射角α=60°，折射角γ=30°，
根据折射定律：n=sinαsinγ=

本题解析：

本题难度：简单

2、计算题  (9分)如图所示，一束截面为圆形(半径R＝1 m)的平行紫光垂直射向一半径也为R的玻璃半球的平面，经折射后在屏幕S上形成一个圆形亮区．屏幕S至球心的距离为D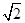＝(＋1) m，不考虑光的干涉和衍射，试问：

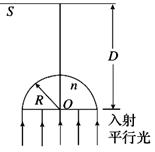
①若玻璃半球对紫色光的折射率为n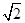＝，请你求出圆形亮区的半径．
②若将题干中紫光改为白光，在屏幕S上形成的圆形亮区的边缘是什么颜色？

参考答案：①1 m　②紫色

本题解析：
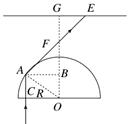①如图，紫光刚要发生全反射时的临界光线射在屏幕S上的点E，E点到亮区中心G的距离r就是所求最大半径．设紫光临界角为C，由全反射的知识：sinC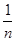＝（1分）
由几何知识可知：AB＝RsinC＝?（1分）? OB＝RcosC＝R（1分）
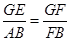BF＝ABtanC＝（1分）? GF＝D－(OB＋BF)＝D－，，（1分）
所以有：rm＝GE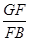＝·AB＝D·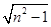－nR＝1 m（2分）
②由于白色光中紫光的折射率最大，临界角最小，故在屏幕S上形成的圆形亮区的边缘应是紫色光．（2分）

本题难度：一般

3、选择题  如图所示，用三块完全相同的两面平行的玻璃板组成一等边三角形（中间是空气），有红光和蓝光组成一细光束以平行底边BC从AB面射入，由AC面射出，则从AC面射出的光束

[? ]
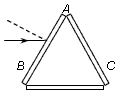
A．分成两束，上面为红光，下面为蓝光
B．分成两束，上面为蓝光，下面为红光
C．仍然为一束，并与底边BC平行
D．仍然为一束，但向底边BC偏折

参考答案：C

本题解析：

本题难度：简单

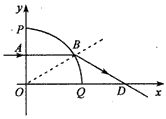
4、计算题  如图所示，在坐标系的第一象限内有一横截面为四分之一圆周的柱状玻璃体OPQ，OP=OQ=R，一束单色光垂直OP面射入玻璃体，在OP面上的入射点为A，OA=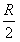，此单色光通过玻璃体后沿BD方向射出，且与 x轴交于D点，OD=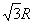，求：
（1）该玻璃的折射率是多少？
（2）将OP面上的该单色光至少向上平移多少，它将不能从PQ面直接折射出来。

参考答案：解：（1）在PQ面上的入射角，θ1=30°
由几何关系可得θ2=60°
折射率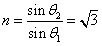

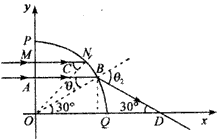
（2）临界角sinC=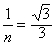
从OP面射入玻璃体的光，在PQ面的入射角等于临界角时，刚好发生全反射而不能从PQ面直接射出。设光在OP面的入射点为M，在PQ面的反射点为N

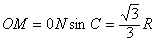
至少向上平移的距离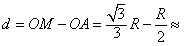0.077R

本题解析：

本题难度：一般

5、计算题  半径为R的玻璃半圆柱体，横截面如图所示，圆心为O 。两条平行单色红光沿截面射向圆柱面方向与底面垂直。光线1的入射点A为圆柱面的顶点，光线 2的入射点B，∠AOB＝60°，已知该玻璃对红光的折射率n＝。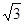

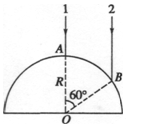
求：（1）两条光线经柱面和底面折射后出射光线的交点与O点的距离d；
（2）若入射的是单色蓝光，则距离d将比上面求得的结果大还是小？（定性分析，不需要计算，画出光路图）

参考答案：（1）；（2）若入射的是单色蓝光，则距离d将比上面求得的结果小

本题解析：
试题分析:光路图如下：

（1）光线1通过玻璃砖后不偏折．光线2在圆柱面上的入射角θ1=60°，由折射定律得 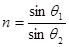?，得到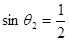，得θ2=30°，由几何知识得：θ1′=60°-θ2=30°，又由折射定律得，代入解得θ2′=60°，由于△BOC是等腰三角形，则，所以。
（2）若入射的单色蓝光，光线1仍不偏折，由于介质对蓝光的折射率大于介质对红光的折射率，光线2偏折得更厉害，θ2′更大，d更小．

本题难度：简单