1、计算题  （10分）一质量m=2kg的小球从光滑斜面上高h=3.5m处由静止滑下，斜面底端紧接着一个半径R=1m的光滑圆环，如图，求：（g=10m/s2）
（1）小球滑至圆环顶点时对环的压力；
（2）小球至少应从多高处静止滑下才能越过圆环顶点．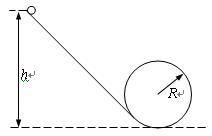

参考答案：（1）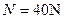
（2）

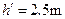
本题解析：（10分）（每问5分）
（1）由动能定理，列方程

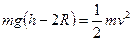
当小球到达在圆环最高点时，有

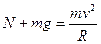
解得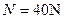
（2）由动能定理，列方程

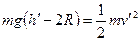
当小球到达在圆环最高点时，有

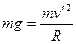
解得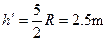

本题难度：简单

2、简答题  一弧形滑道下端与水平传送带相切，一工件从h=1.05高处的A由静止滑下后以水平速度滑上传送带．工件质量m=1.0kg，工件与滑道间平均摩擦阻力的大小f=5.0N，工件滑过的弧长l=2.0m．传送带长L=10m，向右保持v0=2.0m/s的运行速度不变，工件与传送带间的动摩擦因数μ=0.20，g=10m/s2，空气阻力不计，工件可看成质点．
（1）求工件滑上传送带时的速度大小v1=？
（2）求传送带传送一个工件时，克服工件摩擦力所做的功？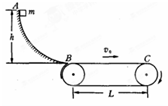

参考答案：（1）工件在弧形轨道上下滑时，
由动能定理得：mgh-fl=12mv12-0，
v1=

本题解析：

本题难度：一般

3、选择题  一个初动能为EK的带电粒子，以速率v垂直电场线方向飞入带电的平行板电容器，飞出时带电粒子动能为飞入时动能的2倍。如果使粒子的初速度为原来的2倍，那么当它飞出电容器的时刻，动能为?（?）
A．4EK
B．4.25EK
C．5EK
D．8EK

参考答案：B

本题解析：设电场宽度为L，电容器间的电场强度为E，粒子第一个过程中初速度为v，则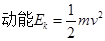?，第一个过程沿电场线方向的位移为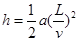：，由动能定理：qEh=2Ek-Ek。第二个过程中沿电场线方向的位移为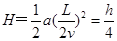，由动能定理qEH=Ekx-4Ek,解得：Ekx=4.25Ek

本题难度：一般

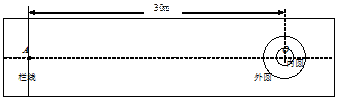
4、简答题  图是新兴的体育比赛“冰壶运动”的场地平面示意图。其中，内圆的半径为0.6 m，外圆的半径为1.8 m，栏线A点距内圆的圆心O点为30 m，比赛时，若参赛一方将已方的冰石壶推至内圆内，并将对方冰石壶击出外圆，则获胜。在某次比赛中，甲队队员以速度v1＝3 m/s将质量为m＝19 kg的冰石壶从左侧栏线A处向右推出，恰好停在O点处。乙队队员以速度v2＝5 m/s将质量为M＝20 kg的冰石壶也从A处向右推出，沿中心线滑动到O点并和甲队冰石壶发生碰撞。设两个冰石壶均可看成质点且碰撞前后均沿中心线运动，不计碰撞时的动能损失，两个冰石壶与水平面的动摩擦因数相同。求：
小题1:冰石壶与冰面间的动摩擦因数；
小题2:?乙队冰石壶能否停在内圆区域内并把甲队冰石壶击出外圆从而获胜。为什么？

参考答案：
小题1:0.015
小题2:即乙获胜。

本题解析：
小题1:由动能定理得：－mmgs＝0－mv12，m＝＝＝0.015；
小题2:?乙队员抛出的冰石壶到达O’点时的速度v’：Mv22－Mv’2＝mMgs，
v’＝＝4 m/s，
两冰石壶发生弹性碰撞（设碰撞后M和m的速度分别为v’’和v3）：
由Mv’＝Mv’’＋mv3和Mv’2＝Mv’’2＋mv32
解得：v3＝v’＝4.1 m/s，v’’＝＝0.1 m/s，
碰撞后，甲冰石壶移动距离s1为mmgs1＝mv32，s1＝＝56 m，
乙冰石壶移动距离s2为s2＝＝0.033 m，甲出外圆，乙在内圆，即乙获胜。

本题难度：一般

5、计算题  滑板项目是极限运动历史的鼻祖，许多的极限运动项目均由滑板项目延伸而来。50年代末60年代初由冲浪运动演变而成的滑板运动，在而今已成为流行运动。 将滑板运动简化成如图所示，AB和CD是一段圆弧形轨道，BC是一段长7m的水平轨道．一运动员从AB轨道上P点以6m/s的速度下滑，经BC轨道后冲上CD轨道，到Q点时速度减为零．已知运动员的质量50kg，h=1.4m，H=1.8m，不计圆弧轨道上的摩擦。（g=10m/s2）求：

（1）运动员第一次经过B点时的速度是多少？
（2）运动员与BC轨道的动摩擦因数？
（3）运动员最后停在BC轨道上距B为多少米处？

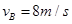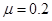参考答案：（1）；（2）；（3）2m

本题解析： ?（1）运动员从P点滑至B点时，由动能定理有 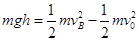?（2分）
解得运动员在B点时的速度?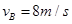?（2分）
（2）运动员由P滑至D过程中，由动能定理有 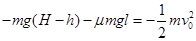?（2分）
解得运动员与BC间的动摩擦因数 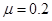?（2分）
（3）设运动员在BC面上滑行的路程为s，从P点开始运动到最后停止，
由能量守恒有?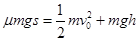?（2分）
解得? s = 16m?（1分）
所以最后停止的位置距离B点为2m?（1分）

本题难度：一般