1、计算题 如图所示,粒子源S可以不断地产生质量为 、电荷量为
、电荷量为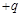 的粒子(重力不计),粒子从
的粒子(重力不计),粒子从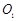 孔漂进(初速不计)一个水平方向的加速电场,再经小孔
孔漂进(初速不计)一个水平方向的加速电场,再经小孔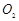 进入相互正交的匀强电场和匀强磁场区域,电场强度大小为
进入相互正交的匀强电场和匀强磁场区域,电场强度大小为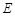 ,磁感应强度大小为
,磁感应强度大小为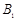 ,方向如图.虚线PQ、MN之间存在着水平向右的匀强磁场,磁感应强度大小为
,方向如图.虚线PQ、MN之间存在着水平向右的匀强磁场,磁感应强度大小为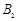 (图中未画出).有一块折成直角的硬质塑料板abc(不带电,宽度很窄,厚度不计)放置在PQ、MN之间(截面图如图),
(图中未画出).有一块折成直角的硬质塑料板abc(不带电,宽度很窄,厚度不计)放置在PQ、MN之间(截面图如图),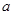 、
、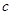 两点恰在分别位于PQ、MN上,
两点恰在分别位于PQ、MN上,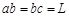 ,
,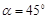 ,现使粒子能沿图中虚线
,现使粒子能沿图中虚线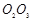 进入PQ、MN之间的区域,求:
进入PQ、MN之间的区域,求:
(1)求加速电压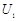 ;
;
(2)假设粒子与硬质塑料板相碰后,速度大小不变,方向变化遵守光的反射定律,粒子在PQ、MN之间的区域中运动的时间和路程分别是多少?

参考答案:(1)
(2)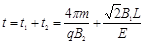
本题解析:(1)粒子源发出的粒子,进入加速电场被加速,速度为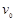 ,根据能的转化和守恒定律得:
,根据能的转化和守恒定律得: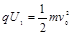 …………①
…………①
要使粒子能沿图中虚线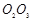 进入PQ、MN之间的区域,则粒子所受到向上的洛伦兹力与向下的电场力大小相等,
进入PQ、MN之间的区域,则粒子所受到向上的洛伦兹力与向下的电场力大小相等,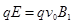 ,解得:
,解得: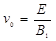 …………②
…………②
将②式代入①式,得 …………③
…………③
(2)粒子从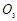 以速度
以速度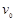 进入PQ、MN之间的区域,先做匀速直线运动,打到ab板上,以大小为
进入PQ、MN之间的区域,先做匀速直线运动,打到ab板上,以大小为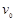 的速度垂直于磁场方向运动。粒子将以半径
的速度垂直于磁场方向运动。粒子将以半径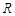 在垂直于磁场的平面内作匀速圆周运动,转动一周后打到ab板的下部,由于不计板的厚度,所以质子从第一次打到ab板到第二次打到ab板后运动的时间为粒子在磁场运动一周的时间,即一个周期
在垂直于磁场的平面内作匀速圆周运动,转动一周后打到ab板的下部,由于不计板的厚度,所以质子从第一次打到ab板到第二次打到ab板后运动的时间为粒子在磁场运动一周的时间,即一个周期 ,
,
由 和运动学公式
和运动学公式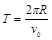 ,解得:
,解得:
粒子在磁场中共碰到2块板,做圆周运动所需的时间为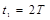
粒子进入磁场中,在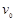 方向的总位移
方向的总位移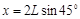 ,时间为
,时间为
则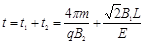
本题难度:简单
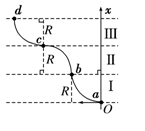
2、选择题 如图5所示,一个质量为m、电荷量为+q的带电粒子,不计重力,在a点以某一初速
度水平向左射入磁场区域Ⅰ,沿曲线abcd运动,ab、bc、cd都是半径为R的圆弧.粒子在每段圆弧上运动的时间都为t.规定垂直于纸面向外的磁感应强度为正,则磁场区域Ⅰ、Ⅱ、Ⅲ三部分的磁感应强度B随x变化的关系可能是图6中的 ( )
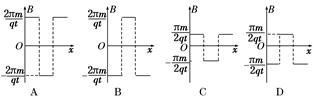
参考答案:C
本题解析:由左手定则可判断出磁感应强度B在磁场区域Ⅰ、Ⅱ、Ⅲ内磁场方向分别为向外、向里、向外,在三个区域中均运动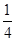 圆周,故t=
圆周,故t= ,由于T=
,由于T=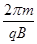 ,求得B=
,求得B= .只有C选项正确.
.只有C选项正确.
本题难度:一般
3、简答题 如图a所示,水平直线MN下方有竖直向下的匀强电场,现将一重力不计、比荷
=106C/kg的负电荷于电场中的.点由静止释放,经过×10-5s后电荷以v0=1.5X104m/sS的速度通过MN进人其上方的均匀磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化.图中以垂直纸面向里为正,电荷通过MN时为t=0时刻.求:
(1)匀强电场的电场强度E及O点与直线MN之间的距离;
(2)如果在O点正右方d=68cm处有一垂直于MN的足够大的挡板,求电荷从O点出发运动到挡板的时间.
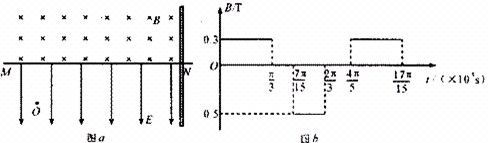
参考答案:(1)电荷在电场中做匀减速直线运动,设其在电场中运动的时间为tE,
根据动量定理可知,mv0=qEtE
解得,E=mvoqtE=4.52π×104N/C=7.2×103N/C
O点与直线MN之间的距离d=12at2E=π2cm=1.57cm
(2)当磁场垂直纸面向里时,
电荷运动的半径r1=mvoqB1=10-6×1.5×1040.3m=5cm
周期T1=2xmqB1=2π×10-60.38=2π3×10-6S
当磁场垂直纸面向外时,
电荷运动的半径r2=mvoqB2=10-6×1.5×1040.5m=3cm
周期T2=2πmqB2=2πmqB2=2π×10-60.55=2π5×10-58
根据电荷的运动情况可知,电荷到达挡板前运动的完整周期数为15个,即沿ON运动的距离S=15△d=60cm,最后8cm的距离
如图所示,r1+r1cosa=d-S
解得cosα=0.6则α=53°
故电荷运动的总时间
T=tk+15TB+12T1-53360T1
=(12+163540)x×10-5S=3.86×10-4S
答:(1)匀强电场的电场强度7.2×103N/C及O点与直线MN之间的距离1.57cm;
(2)如果在O点正右方d=68cm处有一垂直于MN的足够大的挡板,则电荷从O点出发运动到挡板的时间3.86×10-4s.
本题解析:
本题难度:一般
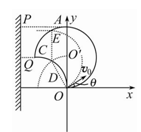
4、计算题 如图所示,质量为m,电荷量为e的电子从坐标原点O处沿xOy平面射入第一象限内,射入时的速度方向不同,但大小均为v0.现在某一区域内加一方向向外且垂直于xOy平面的匀强磁场,磁感应强度大小为B,若这些电子穿过磁场后都能垂直地射到与y轴平行的荧光屏MN上,求:

小题1:电子从y轴穿过的范围;
小题2:荧光屏上光斑的长度;
小题3:所加磁场范围的最小面积.
参考答案:
小题1: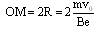
小题2: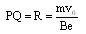
小题3: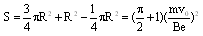
本题解析:(1)设粒子在磁场中运动的半径为R,由牛顿第二定律得: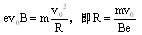
电子从y轴穿过的范围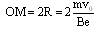
(2)如图所示,初速度沿x轴正方向的电子沿弧OA运动到荧光屏MN上的P点,?
初速度沿y轴正方向的电子沿弧OC运动到荧光屏MN上的Q点
由几何知识可得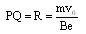
(3)取与x轴正方向成θ角的方向射入的电子为研究对象,其射出磁场的点为E(x,y),因其射出后能垂直打到荧光屏MN上,故有:
x="-Rsinθ?" ?
y="R+Rcosθ?" ?
即x2+(y-R)2=R2?
又因为电子沿x轴正方向射入时,射出的边界点为A点;沿y轴正方向射入时,射出的边界点为C点,故所加最小面积的磁场的边界是以(0,R)为圆心、R为半径的圆的一部分,如图中实线圆弧所围区域,所以磁场范围的最小面积为: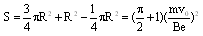
本题难度:一般
5、选择题 在匀强磁场中,一个带电粒子做匀速圆周运动,如果又顺利垂直进入另一磁感应强度是原来磁感应强度2倍的匀强磁场,则
[? ]
A.粒子的速率加倍,周期减半
B.粒子的速率不变,轨道半径减半
C.粒子的速率减半,轨道半径变为原来的1/4
D.粒子的速率不变,周期减半
参考答案:BD
本题解析:
本题难度:一般