1、选择题 如图所示,水平光滑地面上停放着一辆质量为M的小车,其左侧有半径为R的四分之一光滑圆弧轨道AB,轨道最低点B与水平轨道BC相切,整个轨道处于同一竖直平面内。将质量为m的物块(可视为质点)从A点无初速释放,物块沿轨道滑行至轨道末端C处恰好没有滑出。设重力加速度为g,空气阻力可忽略不计。关于物块从A位置运动至C位置的过程,下列说法中正确的是
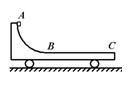
A.小车和物块构成的系统动量不守恒
B.摩擦力对物块和轨道BC所做功的代数和为零
C.物块运动过程 中的最大速度为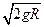
D.小车运动过程中的最大速度为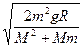
参考答案:AD
本题解析:略
本题难度:一般
2、计算题 如图,水平地面和半圆轨道面均光滑,质量M=1kg的小车静止在地面上,小车上表面与 m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以
m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以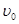 =6m/s的初速度滑上小车左端,二者共速时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,已知滑块与小车表面的滑动摩擦因数μ=0.2,g取10m/s2.
=6m/s的初速度滑上小车左端,二者共速时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,已知滑块与小车表面的滑动摩擦因数μ=0.2,g取10m/s2.
小题1:求小车的最小长度。
小题2:讨论小车的长度L在什么范围,滑块能滑上P点且在圆轨道运动时不脱离圆轨道?

参考答案:
小题1:
小题2: 或
或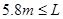 <7m
<7m
本题解析:(1)设滑块与小车的共同速度为v1,滑块与小车相对运动过程中动量守恒,有:
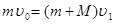 ?……………………………………………………………(2分)
?……………………………………………………………(2分)
代入数据解得: ?…………………………………………………(2分)
?…………………………………………………(2分)
设小车的最小长度为L1,由系统能量守恒定律,有:
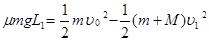 ?……………………………………………(2分)
?……………………………………………(2分)
代入数据解得: ?………………………………………………………(2分)
?………………………………………………………(2分)
(2)设小车与墙壁碰撞时,滑块与P点的距离为L2,若滑块恰能滑过圆的最高点,设滑至最高点的速度为v,临界条件为:
 ?…………………………………………………………………①(2分)
?…………………………………………………………………①(2分)
根据动能定理,有:
 ?……………………………………②(1分)
?……………………………………②(1分)
①②联立并代入数据解得:L2="1m?" ………………………………………………………(1分)
这种情况下小车的长度为: m?
m?
若滑块恰好滑至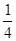 圆弧到达T点时就停止,则滑块也能沿圆轨道运动而不脱离圆轨道.
圆弧到达T点时就停止,则滑块也能沿圆轨道运动而不脱离圆轨道.
根据动能定理,有:
 ?…………………………………………(1分)
?…………………………………………(1分)
代入数据解得: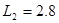 ?m?………………………………………………(1分)
?m?………………………………………………(1分)
这种情况下小车的长度为: m?
m?
若滑块滑至P点时速度恰好为零,由动能定理,有:
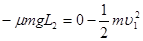 ?………………………………………………………………(1分)
?………………………………………………………………(1分)
解得: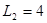 m?………………………………………………………………(1分)
m?………………………………………………………………(1分)
这种情况下小车的长度为: m?
m?
综上所述,滑块能沿圆轨道运动而不脱离圆轨道,半圆轨道的半径必须满足:
 或
或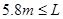 <7m?…………………………………(2分)
<7m?…………………………………(2分)
本题难度:简单
3、计算题 如图所示是某车间用电动滚轮在家具板上压扎浅槽的示意图,已知滚轮半径为R=0.4 m,家具板长L=2.8 m、质量m=10 kg,滚轮与家具板、家具板与工作台面间的动摩擦因数分别为μ1=0.3和μ2=0.1。家具板从一端放人工作台的滚轮下,工作时滚轮对家具板产生恒定的竖直向下的压力,大小为100 N,在滚轮的摩擦力作用下家具板由静止开始向前运动并被压扎出一道浅槽。已知滚轮转动的角速度恒为5 rad/s,g=10 m/s2。
(1)通过分析计算,说明家具板将如何运动。
(2)加工一块家具板需要多长时间?
(3)加工一块家具板电动机要消耗多少电能(不考虑电动机自身的能耗)。

参考答案:解:
(1)家具板受力如图所示, 滚轮与家具板间的滑动摩擦力f1=μ1N1=30 N
?家具板与工作台面间的滑动摩擦力f2= μ2N2=μ2(mg+N1)=20 N
由牛顿第二定律得f1-f2=ma
解得加速度a=1 m/s2
加速过程家具板能达到的最大速度为vm=ωR=2 m/s
这一过程家具板的位移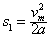 =2 m<2.8 m
=2 m<2.8 m
此后,滚轮给家具板的摩擦力变为静摩擦力,家具板将做匀速运动。
即整个过程中,家具板先以a=1 m/s2的加速度做匀加速运动,达到速度2 m/s后再匀速运动;
(2)家具板加速的时间
家具板匀速运动的时间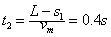
所以,加工一块家具板需要的时间为t=t1+t2=2.4 s
(3)加工一块家具板电动机要消耗的电能为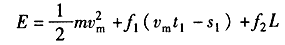
解得E=136 J。
本题解析:
本题难度:一般
4、选择题 如图所示,质量为M、长度为l的小车静止在光滑的水平面上,质量为m的小物块放在小车的最左端。现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动。物块和小车之间的摩擦力的大小为f。经过时间t,小车运动的位移为s,物块刚好滑到小车的最右端。物块可以看成质点,则
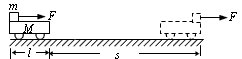
[? ]
A.物块受到的摩擦力对物块做的功与小车受到的摩擦力对小车做功的代数和为零
B.整个过程物块和小车增加的机械能为F(s+l)
C.整个过程物块和小车间摩擦生热为fl
D.小车的末动能为fs
参考答案:CD
本题解析:
本题难度:一般
5、计算题 子弹水平射入静止在光滑的水平面上木块中,进入木块的最大深度为 。若在子弹深入木块直到最大深度的过程中,木块沿桌面移动距离为
。若在子弹深入木块直到最大深度的过程中,木块沿桌面移动距离为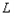 ,木块对子弹平均阻力大小为
,木块对子弹平均阻力大小为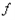 ,那么在这一过程中,求:
,那么在这一过程中,求:
(1)木块动能改变量为多少?
(2)子弹动能改变量为多少?
(3)子弹和木块组成系统机械能损失多少?
参考答案:解:(1 )对木块分析,子弹对木块的作用力对木块做的功等于木块动能的增加量。
即木块动能改变量为 △Ek 木=f ·L
(2 )对子弹分析,木块对子弹的作用力对子弹做的功等于子弹动能的变化。
即子弹动能的变化量是 △Ek子=-f ·( d +L)
也就是系统动能的减少量是 f ·( d +L)?
(3 )子弹和木块组成系统,减少的机械能等于增加的内能(发热量)
而发热量是 Q =f ·L 相对=f?· d
所以系统机械能损失是 E 损=Q =f ·d
本题解析:
本题难度:一般