1、计算题 如图所示,一轻质弹簧两端连着物体A和B,放在光滑的水平面上,物体A被水平速度为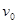 的子弹击中,子弹停在其中,已知A的质量是B的质量的
的子弹击中,子弹停在其中,已知A的质量是B的质量的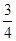 ,子弹的质量是B的质量的
,子弹的质量是B的质量的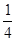 。求:
。求:
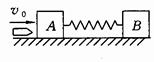
(1)A物体获得的最大速度的大小。
(2)弹簧压缩量最大时B物体的速度大小
参考答案:①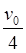 ?②
?②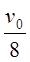
本题解析:子弹和A木块相撞动量守恒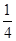 mv0=(
mv0=(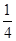 m+
m+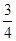 m)v1? v1=
m)v1? v1=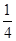 v0
v0
子弹和A组成的系统再和B相碰动量守恒,当弹簧压缩最短时系统各部分速度相等,
(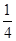 m+
m+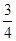 m)v1=(m+
m)v1=(m+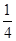 m+
m+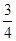 m)v? v=
m)v? v=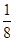 v0
v0
此过程机械能守恒动能的减少量转化为弹性势能。
Ep=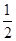 (
(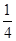 m+
m+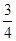 m)v12-
m)v12-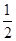 (m+
(m+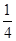 m+
m+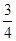 ?)v2=mv02/64
?)v2=mv02/64
本题难度:一般
2、计算题 (9分)如图所示,可看成质点的A物体叠放在上表面光滑的B物体上,一起以v0的速度沿光滑的水平轨道匀速运动,与静止在同一光滑水平轨道上的木板C发生完全非弹性碰撞,B、C的上表面相平且B、C不粘连,A滑上C后恰好能到达C板的最右端,已知A、B、C质量均相等,木板C长为L,求

①A物体的最终速度
②A在木板C上滑行的时间
参考答案:①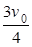 ;②
;②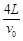
本题解析:①设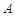 、
、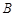 、
、 的质量为
的质量为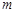 ,
, 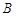 、
、 碰撞过程中动量守恒,
碰撞过程中动量守恒,
令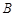 、
、 碰后的共同速度为
碰后的共同速度为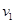 ,则
,则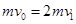 ,解得
,解得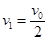 ,?
,?
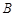 、
、 共速后
共速后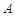 以
以 的速度滑上
的速度滑上 ,
,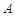 滑上
滑上 后,
后,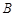 、
、 脱离
脱离
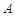 、
、 相互作用过程中动量守恒,设最终
相互作用过程中动量守恒,设最终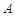 、
、 的共同速度
的共同速度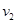 ,
,
则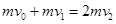 ?
?
解得?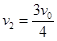 ?
?
②在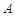 、
、 相互作用过程中,根据功能关系有
相互作用过程中,根据功能关系有
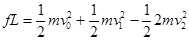 (
(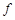 为
为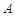 、
、 间的摩擦力)?
间的摩擦力)?
代入解得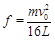 ·?
·?
此过程中对 ,根据动量定理有
,根据动量定理有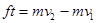 ?
?
代入相关数据解得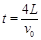
本题难度:一般
3、选择题 如图所示,在水平方向的匀强电场中,一绝缘细线的一端固定在O点,另一端系一带正电的小球,小球在只受重力、电场力、绳子的拉力作用下在竖直平面内做圆周运动,小球所受的电场力大小等于重力大小.比较a、b、c、d这四点,小球 ( )
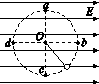
A.在最高点a处的动能最小
B.在最低点c处的机械能最小
C.在水平直径右端b处的机械能最大
D.在水平直径左端d处的机械能最大
参考答案:C
本题解析:由图知,小球从a到d的过程中重力做正功,电场力做负功,因小球所受的电场力大小等于重力大小,且位移都为圆的半径r,所以合力的功为零,即小球的动能不变,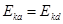 ,A错;因重力做功机械能守恒,所以电场力做正功最大的位置就是机械能最大的位置,在四个点中,小球运动到b点时,电场力做功最大,所以b处的机械能最大,BD错,C对。
,A错;因重力做功机械能守恒,所以电场力做正功最大的位置就是机械能最大的位置,在四个点中,小球运动到b点时,电场力做功最大,所以b处的机械能最大,BD错,C对。
点评:本题学生明确小球在运动的过程中,只有重力和电场力做功,绳对球的拉力不做功。
本题难度:一般
4、选择题 如图所示,固定的光滑倾斜杆上套有一个质量为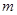 的圆环,圆环与竖直放置的轻质弹簧上端相连,弹簧的下端固定在水平地面上的A点,开始弹簧恰好处于原长
的圆环,圆环与竖直放置的轻质弹簧上端相连,弹簧的下端固定在水平地面上的A点,开始弹簧恰好处于原长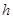 .现让圆环由静止沿杆滑下,滑到杆的底端(未触及地面)时速度恰好为零,已知当地的重力加速度大小为
.现让圆环由静止沿杆滑下,滑到杆的底端(未触及地面)时速度恰好为零,已知当地的重力加速度大小为 .则在圆环下滑的整个过程中
.则在圆环下滑的整个过程中

A.圆环与弹簧和地球组成的系统机械能守恒
B.弹簧的弹性势能先增大后减小
C.弹簧的弹性势能增大了
D.弹簧的最大压缩量小于其最大伸长量
参考答案:ACD
本题解析:考点:
分析:分析圆环沿杆下滑的过程的受力和做功情况,只有重力弹簧的拉力做功,所以圆环机械能不守恒,但是系统的机械能守恒;沿杆方向合力为零的时刻,圆环的速度最大.
解答:解:A、圆环沿杆滑下,滑到杆的底端的过程中有两个力对圆环做功,即环的重力和弹簧的拉力;所以圆环的机械能不守恒,如果把圆环和弹簧组成的系统作为研究对象,则系统的机械能守恒,故A选项正确,
B、弹簧的弹性势能随弹簧的形变量的变化而变化,由图知弹簧先缩短后再伸长,故弹簧的弹性势能先增大再减小后增大才对.故B选项错误.
C、根据系统的机械能守恒,圆环的机械能减少了mgh,那么弹簧的机械能即弹性势能增大mgh.故C选项正确.
D、由图可知,弹簧的最大压缩量在弹簧与杆垂直的时刻,此时的系统具有的能量为圆环的动能、势能和弹簧的弹性势能,当圆环速度减为零时,到达最底端,此时圆环的动能和势能都为零,系统所有的机械能全部转化成了弹簧的弹性势能,此时的弹簧处于伸长状态,所以弹簧的最大伸长量要大于最大压缩量,故D正确.
故选A、C、D.
点评:对物理过程进行受力、运动、做功分析,是解决问题的根本方法.这是一道考查系统机械能守恒的基础好题.
本题难度:简单
5、计算题 如图所示,光滑水平面上有一静止小车B,左端固定一砂箱,砂箱的右端连接一水平轻弹簧,小车与砂箱的总质量为M1=1.99 kg.车上静置一物体A,其质量为M2=2.00 kg.此时弹簧呈自然长度,物体A的左端的车面是光滑的,而物体A右端的车面与物体间的动摩擦因数为μ=0.2.现有一质量为m=0.01 kg的子弹以水平速度v0=400 m/s打入砂箱且静止在砂箱中,求:

(1)小车在前进过程中,弹簧弹性势能的最大值.
(2)为使物体A不从小车上滑下,车面的粗糙部分至少多长?(g取10 m/s2)
参考答案:(1)2 J (2)0.5 m
本题解析:(1)子弹射入砂箱后,子弹、砂箱和小车获得共同的速度,设为v1,以子弹、砂箱和小车组成的系统为研究对象,根据动量守恒定律,有
mv0=(M1+m)v1
之后,小车与A通过弹簧作用又达到共同速度,设为v2,此时弹簧压缩最大,则对子
弹、砂箱和小车以及物体、弹簧整个系统,根据动量守恒定律,有
(M1+m)v1=(M1+M2+m)v2
根据能量守恒,有
Ep=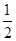 ?(M1+m)v12-
?(M1+m)v12-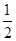 ?(M1+m+M2)v22
?(M1+m+M2)v22
联立以上三式得
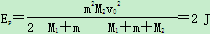 .
.
(2)A被压缩的弹簧向右推动直到脱离弹簧后,又通过摩擦力与小车作用再次达到共同
速度,设为v3,对小车与A组成的系统,根据动量守恒定律,有
(M1+M2+m)v2=(M1+M2+m)v3
由此得v2=v3;而对物体A和弹簧组成的系统,根据功能关系,有μM2gs=Ep
解得s=0.5 m.
点评:本题涉及到弹簧,功、机械能守恒的条件、力和运动的关系等较多知识.题目情景比较复杂,全面考查考生理解、分析、解决问题的能力.
本题难度:一般