1、填空题  在研究平抛物体运动的实验中，用一张印有小方格的纸记录轨迹，小方格的边长L=2.5cm。若小球在平抛运动途中的几个位置如图中的a、b、c、d所示，则

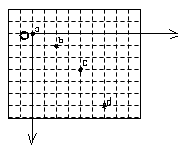
（1）小球平抛的初速度的计算式为V0=_____________（用L、g表示），其值是________
（2）小球经过b速度的计算式为Vb=_____________

（用L、g表示），其值是________
（3）小球开始做平抛运动的位置坐标为：x＝___________cm? y＝___________cm

参考答案：（1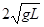），1m/s,　(2) 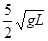,1.25m/s,　　(3)-2.5,-0.31

本题解析：分析：平抛运动分解为：水平方向的匀速直线运动，竖直方向的自由落体运动．从小方格的纸记录轨迹可看出，从a→b→c→d的水平位移一样，都为2L，说明各段的时间相等，设为T，可知2L=v0T，由运动的等时性，T由竖直方向运动求出，从a→b→c→d的竖直位移依次相差L，由匀变速直线运动的规律得L=gT2，联立可求出初速度v0．再有中间时刻的瞬时速度等于这段
时间的平均速度规律求出b的竖直速度vby，然后运用运动的合成求出b的速度vb．
利用vby=vay+gT和vay=gt求出从抛出到a点的时间t，这样可求出从抛出到a点的水平位移x=v0t和竖直位移y=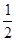gt2，那么就可以求出小球开始做平抛运动的位置坐标（x，y分别在x轴、y轴的负半轴，应为负值．）．
解答：解：（1）、从小方格的纸记录轨迹可看出从a→b→c→d的水平位移一样，都为2L，说明各段的时间相等，设为T，可知：? 2L=v0T，分析a→b→c→d的竖直位移依次相差L，由匀变速直线运动的规律得：L=gT2，联立可求出初速度v0=2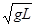，代入数值得v0=2×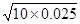m/s=1.0m/s．
（2）、由中间时刻的瞬时速度等于这段时间的平均速度得b的竖直速度vby==，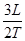
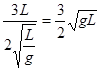运用运动的合成求出b的速度：vb=，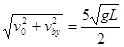
代入数值得：vb=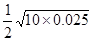m/s=1.25m/s．
（3）b点的竖直方向速度：vby=vay+gT，
∴vay=vby-gT=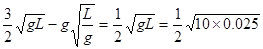m/s=0.25m/s，又vay=gt，∴从抛出到a点的时间t=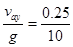s=0.025s，因此从抛出到a点的水平位移x=v0t=1.0×0.025 m=0.025m=2.5cm，
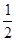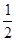竖直位移y=gt2=×10×(0.025)?m=0.003125m=0.3125cm，
那么小球开始做平抛运动的位置坐标（-2.5cm，-0.3125cm）．
故答案：（1）2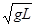，1m/s；（2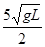），1.25m/s；（3）-2.5cm，-0.3125cm
点评：平抛运动分解为：水平方向的匀速直线运动，竖直方向的自由落体运动．分析小球水平方向和竖直方向的运动特点，充分利用匀变速直线运动的规律结合运动的合成来求解，所求的坐标为负值．

本题难度：简单

2、填空题  （7分）质量为 m的物体从高h 处以速度v水平抛出，该处的重力加速度为g，则物体从抛出到落地所用时间为?①?，落地时水平位移为?②?，落地时的物体竖直方向速度为?③?，落地时物体的速度?④?，落地速度与水平方向夹角的正切值为?⑤?；从抛出到落地物体重力势能减小了?⑥?，落地瞬间重力做功的瞬时功率?⑦?．

参考答案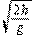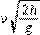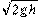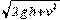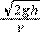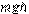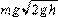：?；?；?；?；；；? (每空1分)

本题解析：略

本题难度：简单

3、选择题  一物体从某高度以初速度v0水平抛出，落地时速度大小为v，则它运动的时间为
[? ]
A.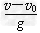
B.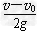
C.
D.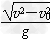

参考答案：D

本题解析：

本题难度：简单

4、简答题  如图a所示是“研究平抛物体的运动”的实验装置图．

（1）图b是正确实验后的数据，其中O为抛出点，则此小球做平抛运动的初速度为______m/s．
（2）在另一次实验中将白纸换成方格纸，方格边长L=5cm，通过实验，记录了小球在运动途中的三个位置，如图c所示，则该小球做平抛运动的初速度为______m/s；B点的竖直分速度为______m/s．

参考答案：（1）因为O点是抛出点，则h=12gt2，t=

本题解析：

本题难度：一般

5、选择题  关于平抛运动，下列说法正确的是（?）
A：平抛运动是匀变速运动?
B：平抛运动是变加速运动
C：任意两段时间内加速度相同?
D：任意两段相等时间内速度变化相同

参考答案：ACD

本题解析：平抛运动中物体只受重力作用，加速度恒定是匀变速曲线运动，B错

本题难度：简单