1、选择题  关于动能，下列说法中正确的是（　　）
A．只要物体的质量发生变化，其动能一定随着变化
B．只要物体的速度发生变化，其动能一定随着变化
C．物体所受合力不为零时，其动能一定发生变化
D．物体所受合力做的功不为零时，其动能一定发生变化

参考答案：A、由动能的计算式Ek=12mv2可知物体质量变化时，动能不一定变化．故A错误．
? B、动能只与速度的大小有关．速度是矢量，若速度不变，方向变化时，速度是变化，而动能不变．故B错误．
? C、合力不为零，合力的功可能为零，动能可能不变，比如匀速圆周运动．故C错误．
? D、根据动能定理：合力的功等于物体动能的变化，可知：合力做的功不为零时，其动能一定发生变化．
故选D

本题解析：

本题难度：一般

2、计算题  如图所示，某货场利用固定于地面的、半径R=l.8m的四分之一圆轨道将质量为m1=10kg的货物（可视为质点）从高处运送至地面，已知当货物由轨道顶端无初速滑下时，到达轨道底端的速度为5m/s。为避免货物与地面发生撞击，在地面上紧靠轨道依次排放两块完全相同的木板A、B，长度均为l=2m，质量均为m2=20 kg，木板上表面与轨道末端相切，货物与木板间的动摩擦因数为μ1= 0.4，木板与地面间的动摩擦因数μ2=0.1。（最大静摩擦力与滑动摩擦力大小相等，取g=10 m/s2）
（1）求货物沿圆轨道下滑过程中克服摩擦力做的功；
（2）通过计算判断货物是否会从木板B的右端滑落？若能，求货物滑离木板B右端时的速度；若不能，求货物最终停在B板上的位置。

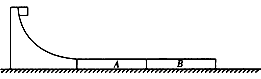
参考答案：解：（1）设货物沿圆轨道下滑过程中克服摩擦力做的功为Wf。
对货物，由动能定理得：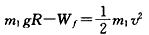
?
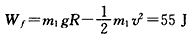
（2）当货物滑上木板A时，货物对木板的摩擦力f1=μm1g=40N
地面对木板A、B的最大静摩擦力f2=μ2(2m2+m1)g=50N
由于f1＜f2，此时木板A、B静止不动设货物滑到木板A右端时速度为v1，
由动能定理：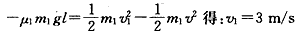
当货物滑上木板B时，地面对木板A、B的最大静摩擦力f3=μ(m2+m1)g=30N
由于f1> f3，此时木板B开始滑动设货物不会从木板B的右端滑落，二者刚好相对静止时的速度v2，
则对货物有：a1=μ1g=4m/s2
v2=v1-a1t，对木板B有：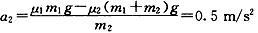
v2=a2t 由以上两式可得：，
此过程中，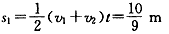

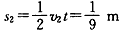
由于s1-s2 =1.0m＜l，所以货物最终未从木板B上滑出，且与其右端的距离为1.0m。

本题解析：

本题难度：困难

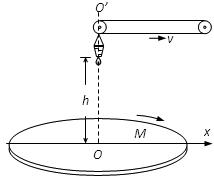
3、计算题  如图所示，是水平放置的半径足够大的圆盘，绕过其圆心的竖直轴匀速转动，规定经过圆心O水平向右为x轴的正方向．在圆心O正上方距盘面高为h处有一个正在间断滴水的容器，从t＝0时刻开始随传送带沿与x轴平行的方向做匀速直线运动，速度大小为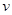.已知容器在t＝0时刻滴下第一滴水，以后每当前一滴水刚好落到盘面上时再滴一滴水．求：
?
(1)每一滴水经多长时间滴落到盘面上？
(2)要使每一滴水在盘面上的落点都位于同一直线上，圆盘转动的角速度ω应为多大？
(3)第二滴水与第三滴水在盘面上落点间的最大距离x.

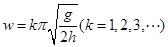参考答案：（1）?（2）?（3）

本题解析：（1）水滴在竖直方向做自由落体运动，有：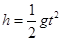
解得
（2）在一滴水的下落时间内，圆盘转过的最小角度为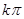，所以最小角速度为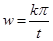
解得：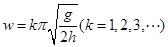
（3）第二滴水落在圆盘上的水平位移为?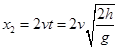
第三滴水在圆盘上的水平位移为?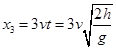
当第二滴水与第三滴水在盘面上的落点位于同一直径上圆心的两侧时，两点间的距离最大，
则：
解得：

本题难度：一般

4、简答题  如图所示是两对接的轨道，两轨道与水平面的夹角均为α=30°，左轨道光滑，右轨道粗糙．一质点自左轨道上距O点L0处从静止起滑下，当质点第一次返回到左轨道并达到最高点时，它离O点的距离为

参考答案：设质点在右轨道上滑距离为L
? 根据动能定理，得
? 从左向右过程：mg（L0-L）sinα-μmgcosα?L=0? ①
? 从右向左过程：mg（L-L03）sinα-μmgcos?L=0? ②
? 由①-②得
? ?L=23L0
? 代入①解得μ=

本题解析：

本题难度：一般

5、简答题  如图1所示，轻弹簧一端固定在与斜面垂直的挡板上，另一端点在O位置．质量为m的物块A（可视为质点）以初速度v0从距O点为x0的P点沿斜面向下运动，与弹簧接触后压缩弹簧，将弹簧右端压到O′点位置后，A又被弹簧弹回．A离开弹簧后，恰好回到P点．物块A与斜面间的动摩擦因数为μ，斜面倾角为37°．求：
（1）O点和O′点间的距离x1．
（2）如图2若将另一个与A完全相同的物块B（可视为质点）与弹簧右端拴接，将A与B并排在一起，使弹簧仍压缩到O′点位置，然后从静止释放，A、B共同滑行一段距离后分离．分离后物块A沿斜面向上滑行的最大距离x2是多少？

参考答案：（1）A从向下运动到再次返回到P的过程，根据动能定理有：
2μmg(x0+x1)=12mv02
解得：x1=5v0216μg-x0
（2）A从O′到P过程设弹簧弹力做功为W，根据动能定理有：
W-μmg（x0+x1）cosθ-mgsinθ（x0+x1）=0
A、B将在弹簧原长处分离，设此时共同速度为v，根据动能定理有：W-2μmgx1cosθ-2mgx1sinθ=122mv12
分离后对A有：μmgx2cosθ+mgx2sinθ=12mv12
联立以上各式可得：x2=x0-5v0232μg．
答：（1）O点和O′点间的距离x1=5v0216μg-x0．
（2）分离后物块A沿斜面向上滑行的最大距离x2是x2=x0-5v0232μg．

本题解析：

本题难度：一般