1、简答题 经过天文望远镜的长期观测,人们在宇宙中已经发现了许多双星系统,通过对它们的研究,使我们对宇宙中的物质的存在形式和分布情况有了较深刻的认识.双星系统是由两个星体组成,其中每个星体的线度都远小于两个星体之间的距离.一般双星系统距离其他星体很远,可以当作孤立系统处理.现根据对某一双星系统的光学测量确定,该双星系统中每个星体的质量都是M,两者间距L,它们正围绕着两者连线的中点作圆周运动.
(1)试计算该双星系统的周期T;
(2)若实验上观测到的运动周期为T’,为了解释两者的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质.作为一种简化模型,我们我们假定在以两个星体连线为直径的球体内均匀分布着密度为ρ的暗物质,而不考虑其它暗物质的影响,并假设暗物质与星体间的相互作用同样遵守万有引力定律.试根据这一模型计算双星系统的运动周期T’.
参考答案:(1)以双星系统中任一星球为研究对象,根据万有引力提供向心力,
由牛顿第二定律得
GM2L2=Mr1ω2=Mr2ω2r1=r2=L2T=2π
本题解析:
本题难度:一般
2、选择题 把火星和地球绕太阳运行的轨道视为圆周,由火星和地球绕太阳运动的周期之比可求得( )
A.火星和地球的质量之比
B.火星和太阳的质量之比
C.火星和地球绕太阳公转轨道半径之比
D.火星和地球绕太阳运行速度大小之比
参考答案:A、我们研究火星和地球绕太阳做圆周运动,火星和地球作为环绕体,无法求得火星和地球的质量之比,故A错误;
B、只知道火星和地球绕太阳运动的周期之比,不能求得火星和太阳的质量之比,列式的时候火星的质量约去了,故B错误;
C、研究火星和地球绕太阳做圆周运动,根据万有引力提供向心力,列出等式:
GMmr2=m4π2rT2,
得T=2π
本题解析:
本题难度:一般
3、选择题 某同学在学习中记录了一些与地球、月球有关的数据资料如表中所示,利用这些数据来计算地球表面与月球表面之间的距离s,则下列运算公式中正确的是( )
地球半径
| R="6" 400 km
|
月球半径
| r="1740" km
|
地球表面重力加速度
| g0=9.80m/s2
|
月球表面重力加速度
| g′=1.56m/s2
|
月球绕地球转动的线速度
| v="1" km/s
|
月球绕地球转动的周期
| T=27.3天
|
光速
| c=2.998×108km/s
|
用激光器向月球表面发射激光光束,经过约t="2.565" s接收到从月球表面反射回来的激光信号
|
A. B.
B.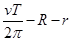
C. D.
D.
参考答案:ABD
本题解析:用光速与激光到达月球的时间的乘积可得地月表面的距离,即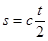 ;月球绕地球做圆周运动的轨道半径为
;月球绕地球做圆周运动的轨道半径为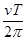 ,然后减去地球及月球的半径R、r,也可得地球表面与月球表面之间的距离s,即s=
,然后减去地球及月球的半径R、r,也可得地球表面与月球表面之间的距离s,即s=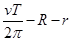 ;根据
;根据 ,其中
,其中 ,解得r1=
,解得r1=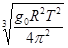 ,所以地球表面与月球表面之间的距离s=r1-r-R=
,所以地球表面与月球表面之间的距离s=r1-r-R= .选项ABD正确。
.选项ABD正确。
考点:万有引力定律及其应用。
本题难度:一般
4、选择题 把火星和地球绕太阳运行的轨道视为圆周,由火星和地球绕太阳运动的周期之比可求得(?)
A.火星和地球的质量之比
B.火星和太阳的质量之比
C.火星和地球到太阳的距离之比
D.火星和地球绕太阳运行速度大小之比
参考答案:CD
本题解析:火星和地球绕太阳运行的轨道视为圆周,则做匀速圆周运动,则由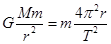 ,
,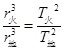 ,则A、B选项错误,C选项正确;
,则A、B选项错误,C选项正确;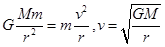 ,可求出火星和地球绕太阳运行速度大小之比,D选项正确。
,可求出火星和地球绕太阳运行速度大小之比,D选项正确。
本题难度:一般
5、选择题 假设地球的质量不变,半径增大到原来的2倍,那么从地球发射人造卫星的第一宇宙速度的大小应为原来的
A.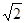 倍
倍
B. 倍
倍
C.1/2倍
D.2倍
参考答案:B
本题解析:根据万有引力定律及牛顿第二定律有: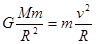 ,解得从地球发射人造卫星的第一宇宙速度
,解得从地球发射人造卫星的第一宇宙速度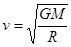 ,在质量不变的情况下
,在质量不变的情况下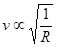 ,故当半径增大为原来的2倍时,第一宇宙速度变为原来的
,故当半径增大为原来的2倍时,第一宇宙速度变为原来的 倍,所以只有B正确。
倍,所以只有B正确。
本题难度:一般