1、计算题 (20分)一半径R=0.6m的金属圆筒有一圈细窄缝,形状如图所示。圆筒右侧与一个垂直纸面向里的有界匀强磁场相切于P,圆筒接地,圆心O处接正极,正极与圆筒之间的电场类似于正点电荷的电场,正极与圆筒之间电势差U可调。正极附近放有一粒子源(粒子源与正极O间距离忽略不计)能沿纸面向四周释放比荷q/m=1.5×l05C/kg的带正电粒子(粒子的初速度、重力均不计)。带电粒子经电场加速后从缝中射出进入磁场,已知磁场宽度d=0.4m,磁感应强度B=0.25T。
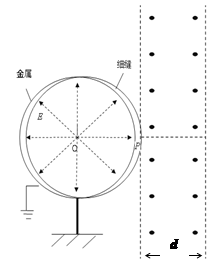
(1)若U=750V,求:①粒子达到细缝处的速度;②若有一粒子在磁场中运动的时间最短,求此粒子飞出磁场时与右边界的夹角大小。
(2)只要电势差U在合适的范围内变化,总有从向沿某一方向射出粒子经过磁场后又回到O处,求电势差U合适的范围。
参考答案:(1)① ②600;(2)
②600;(2)
本题解析:(1)①若U=750V,粒子经电场得
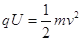 ?(2分)
?(2分)
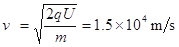 ?(1分)
?(1分)
②粒子在磁场中做匀速圆周运动得 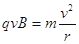 (2分)
(2分)
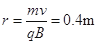 ?(1分)
?(1分)

粒子在磁场中运动轨迹对应的弦长L=d=0.4m时运动的时间最短,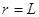 (2分)?
(2分)?
则粒子飞出磁场时与右边界的夹角大小?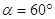 ?(2分)
?(2分)

(2)粒子射入磁场后与右边界相切时,正极与圆筒之间电势差最大为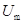 ,由几何关系得
,由几何关系得
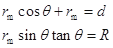 ?(2分)
?(2分)
得? ,
, ?(1分)
?(1分)
粒子在磁场中?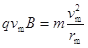 ?(2分)
?(2分)
 ?(1分)
?(1分)
粒子经电场中?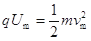 ?(2分)
?(2分)
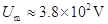 ?(1分)
?(1分)
电势差U合适的范围: ?(1分)
?(1分)
本题难度:一般
2、选择题 关于电荷守恒定律,下列叙述中不正确的是(? )
A.任何一个物体所带的电荷量总是守恒的
B.在与外界没有电荷交换的情况下,一个系统所带的电荷总量是守恒的
C.在一定的条件下,一个系统内等量的正负电荷可以中和,这并不违背电荷守恒定律
D.电荷守恒定律并不意味着带电系统一定和外界没有电荷交换
参考答案:A
本题解析:守恒是指与外界没有电荷交换的情况下成立,所以当物体与外界有电荷有交换时对于一个物体来说电荷就是不守恒的。∴A正确,BCD错误。
本题难度:简单
3、选择题 如下图所示,A板发出的电子经加速后,水平射入水平放置的两平行金属板间,金属板间所加的电压为U,电子最终打在荧光屏P上,关于电子的运动,则下列说法中正确的是( )
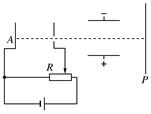
A.滑动触头向右移动时,其他不变,则电子打在荧光屏上的位置下降
B.滑动触头向左移动时,其他不变,则电子打在荧光屏上的位置上升
C.电压U增大时,其他不变,则电子打在荧光屏上的速度大小不变
D.电压U增大时,其他不变,则电子从发出到打在荧光屏上的速度变大
参考答案:D
本题解析:设加速电压为 ,进入偏转电场时的速度为
,进入偏转电场时的速度为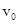 ,则电子经加速电场:
,则电子经加速电场: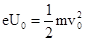 ①
①
偏转电场中: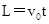 ②
②
 ③
③
 ④
④
由①②③得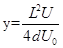
当滑动触头向右滑动时, 变大,y变小,由于粒子是向下偏转的,故电子打在荧光屏上的位置上升,
变大,y变小,由于粒子是向下偏转的,故电子打在荧光屏上的位置上升,
当滑动触头向右滑动时, 变小,y变大,由于粒子是向下偏转的,故电子打在荧光屏上的位置下降,所以选项A、B均错.
变小,y变大,由于粒子是向下偏转的,故电子打在荧光屏上的位置下降,所以选项A、B均错.
对①②③④得
当U增大时, 增大,电子打到屏上的速度变大,故选项C错,D对.
增大,电子打到屏上的速度变大,故选项C错,D对.
故选D
点评:电子在加速电场作用下做加速运动,运用动能定理可得电子获得的速度与加速电场大小间的关系,电子进入偏转电场后,做类平抛运动,运动时间受电场的宽度和进入电场时的速度所决定,电子在电场方向偏转的距离与时间和电场强度共同决定.熟练用矢量合成与分解的方法处理类平抛运动问题.
本题难度:简单
4、简答题 右下图为示波器的部分构造示意图,真空室中阴极K不断发出初速度可忽略的电子,电子经电压为U0的电场加速后,由孔N沿长为I、相距为d的两平行金属板A、B间的中心轴线进入两板间,电子穿过A、B后最终可打在中心为O的荧光屏CD上。若在AB间加上变化规律为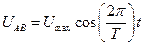 的交变电压,恰好能让t=0时刻进入AB间的电子经A板右边缘射出打在荧光屏上。假设在电子通过两板的极短时间内AB间电场可视为恒定不变。已知电子电荷量为e,质量为m,电子所受重力不计。求:
的交变电压,恰好能让t=0时刻进入AB间的电子经A板右边缘射出打在荧光屏上。假设在电子通过两板的极短时间内AB间电场可视为恒定不变。已知电子电荷量为e,质量为m,电子所受重力不计。求:
(1)电子通过孔N时的速度大小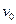 ;
;
(2)A、B间电压的最大值Umax和有效值U。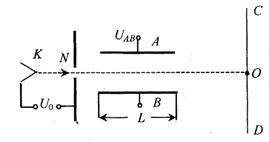
参考答案:
(1)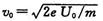 (2)
(2)
本题解析:

本题难度:一般
5、选择题 三个分别带有正电、负电和不带电的相等质量的颗粒,从水平放置的平行带电金属板左侧以相同速度v0垂直电场线方向射入匀强电场,分别落在带正电荷的下板上的a、b、c三点,如图所示,下面判断正确的是
?
A.落在a点的颗粒带正电、c点的带负电、b点的不带电
B.落在a、b、c点颗粒在电场中的加速度的关系是aa>ab>ac
C.三个颗粒在电场中运动所受合力的冲量关系是Ia>Ib>Ic
D.电场力对落在c点的颗粒做负功
参考答案:BCD
本题解析:落在a点的颗粒带负电、c点的带正电、b点的不带电.【命题主旨】考查力、电综合应用.
本题难度:简单