1、简答题 如图所示,ABC为固定在竖直面内的光滑四分之一圆轨道,其半径为r=10m,N为固定在水平面内的半圆平面,其半径为R=
m,轨道ABC与平面N相切于c点,DEF是包围在半圆平面N周围且垂直于N的光滑半圆形挡板,质量为M=1kg的滑块的上表面与平面N在同一水平面内,且滑块与N接触紧密但不连接,现让物体自A点由静止开始下滑,进入平面N后受到挡板DEF的约束并最终冲上滑块,已知m=1kg,物体与平面N之间的动摩擦因数为μ1=0.5、与滑块之间的动摩擦因数为μ2=0.4,滑块与地面之间是光滑的,滑块的竖直高度为h=0.05m,长L=4m.(取g=10m/s2)
(1)物体滑到C处时对圆轨道的压力是多少?
(2)物体运动到F处时的速度是多少?
(3)当物体从滑块上滑落后到达地面时,物体与滑块之间的距离是多少?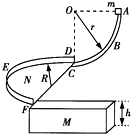
参考答案:(1)对m从A到C?的过程,由动能定理得:mgr=12mvC2
由牛顿第二定律得:
N-mg=mvC2r
? 联立代入数值得:N=3mg=30N?
?由牛顿第三定律m在C处对圆轨道的压力为30N
(2)对m从C到F?
πRμ1mg=12mvC2-12mvF2?
?解得:vF=10m/s?
(3)根据牛顿第二定律,
? 对m:-μ2mg=ma1,解得:a1=-4m/s2?
? 对M:μ2mg=Ma1,解得:a2=4m/s2
设经t时间m刚要从M上滑落,此时m的速度v1,运动的位移为s1,M的速度v2,运动的位移为s2
?s1=vFt+12a1t2
?s2=12a2t2
? 而?s1-s2=L?
由以上三式得:t1=2s,t2=12s
检验:当t1=2s时?v1=vF+a1t1=2m/s,v2=a2t1=8m/s? 不合题意舍去,
当t2=12s时,v1=vF+a1t2=8m/s,v2=a2t2=2m/s?
设m从抛出到落地时间为t3,
? 则h=12gt32
? 解得:t3=0.1s
这段时间内,m水平位移s3=v1t3=0.8m?
? M水平位移?s4=v2t3=0.2m
? 所以△s=s3-s4=0.6m
?答:(1)物体滑到C处时对圆轨道的压力是30N;
(2)物体运动到F处时的速度是10m/s;
(3)当物体从滑块上滑落后到达地面时,物体与滑块之间的距离是0.6m.
本题解析:
本题难度:一般
2、选择题 关于匀速圆周运动的性质,以下说法中正确的是:( ? )
A.匀速运动
B.匀变速运动
C.变加速运动
D.以上说法都不对
参考答案:C
本题解析:
本题难度:简单
3、简答题 如图所示,在xOy平面的y轴左侧存在沿y轴正方向的匀强电场,y轴右侧区域Ⅰ内存在磁感应强度大小B1=
、方向垂直纸面向外的匀强磁场,区域Ⅰ、区域Ⅱ的宽度均为L,高度均为3L.质量为m、电荷量为+q的带电粒子从坐标为(-2L,-L)的A点以速度v0沿+x方向射出,恰好经过坐标为[0,-(-1)L]的C点射入区域Ⅰ.粒子重力忽略不计.
(1)求匀强电场的电场强度大小E;
(2)求粒子离开区域Ⅰ时的位置坐标;
(3)要使粒子从区域Ⅱ上边界离开磁场,可在区域Ⅱ内加垂直纸面向内的匀强磁场.试确定磁感应强度B的大小范围,并说明粒子离开区域Ⅱ时的速度方向.
参考答案:(1)带电粒子在匀强电场中做类平抛运动
则有:
? x轴方向:2L=v0t
? y轴方向:L=12qEm(2Lv0)2
解得:E=mv202qL
(2)设带电粒子经C点时的竖直分速度为?vy、速度为v

则有:vy=qEmt=qEm2Lv0=v0
?所以 v=
本题解析:
本题难度:一般
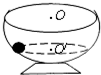
4、选择题 如图所示,O为内表面光滑半球形碗的球心,一小球在碗的内表面沿某一水平面做匀速圆周运动,圆心为O′.关于小球做圆周运动的向心力,下列说法正确的是( )
A.向心力仅由小球受到的重力提供
B.向心力由小球受到的支持力、重力的合力提供
C.向心力的方向指向O′
D.向心力的方向指向O