1、简答题  如图所示，横截面积为S的汽缸A与容器B用一个带有阀门K的细管相连，K闭合时，容器B为真空．用密闭且不计摩擦的活塞将一定质量的理想气体封闭在汽缸A中，活塞上放有若干个质量不同的砝码，当汽缸A中气体的压强为P、温度为T时，活塞离汽缸底部的高度为H，如图所示．现打开阀门K，活塞下降，同时对气体加热，使A、B中气体温度均升至T′，此时活塞离汽缸底高度为4H/5．若要使A、B中气体的温度恢复到T，活塞距离汽缸底部的高度仍然为4H/5，可将活塞上的砝码取走少许，
问：（1）容器B的容积VB多大？
（2）取走的砝码的质量为多少？

参考答案：（1）气体进入B中的过程是等压变化，根据盖-吕萨克定律，有：V1T1=V2T2，
即?HST=45HS+VBT′；
解得：VB=（T′T-45）HS
（2）取走砝码后，保持活塞的高度不变是等容变化，由查理定律　P1T1=P2T2，
得?PT′=P-△mgST；
即△m=(T′-T)pSTg；
答：（1）容器B的容积为（T′T-45）HS；
（2）取走的砝码的质量为(T′-T)pSTg．

本题解析：

本题难度：一般

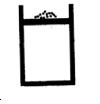
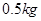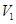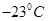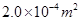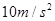2、计算题  (10分)内壁光滑的导热气缸竖直浸放在盛有27℃温水的恒温水槽中，用不计质量的活塞封闭了压强为、体积为的理想气体。现在活塞上方缓缓倒上质量为的沙子，封闭气体的体积变为；然后将气缸移出水槽，经过缓慢降温，气体温度最终变为。已知活塞面积为，大气压强为，g取，求：

(i)气体体积V1．
(ii)气缸内气体的最终体积V2(结果保留两位有效数字)．

参考答案：（1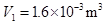）（2）

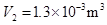
本题解析：(ⅰ)气缸在水槽中，往活塞上方缓缓倒沙子过程中，气体发生等温变化
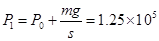Pa ?①
根据玻意耳定律有
?②
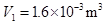解得：??③
（ⅱ）移除水槽后，气体发生等压变化，根据盖-吕萨克定律得：
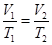?④
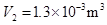解得：??⑤
评分参考：第(ⅰ)问6分，①②③式各2分；第(ⅱ)问4分，④⑤式各2分。

本题难度：一般

3、计算题  一气象探测气球，在充有压强为1.00atm(即76.0cmHg)、温度为27.0℃的氦气时，体积为3.50 m3。在上升至海拔6.50km高空的过程中，气球内氦气逐渐减小到此高度上的大气压36.0cmHg，气球内部因启动一持续加热装置而维持其温度不变。此后停止加热，保持高度不变。已知在这一海拔高度气温为－48.0℃。求：
(1)氦气在停止加热前的体积；
(2)氦气在停止加热较长一段时间后的体积。

参考答案：解:(1)在气球上升至海拔6.50km高空的过程中，气球内氦气经历一等温过程。
根据玻意耳定律有
p1V1＝p2V2
式中，p1＝76.0cmHg，V1＝3.50m3，p2＝36.0cmHg，V2是在此等温过程末氦气的体积。由上式得
V2＝7.39m3
(2)在停止加热较长一段时间后，氦气的温度逐渐从T1＝300K下降到与外界气体温度相同，即T2＝225K。这是一等压过程。根据盖－吕萨克定律有
＝
式中，V3是在此等压过程末氦气的体积。由上式得
V3＝5.54m3

本题解析：

本题难度：一般

4、简答题  如图所示，在很细的U型管两端连着两个容积相等的容器A和B，内装有温度为T0的理想气体．管内两边水银柱高度差为h，当温度降低△T时，两边水银面各移动了多少距离?

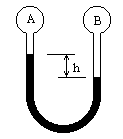
参考答案：

本题解析：

本题难度：简单

5、简答题  一端开口的钢制圆筒在开口端放一轻活塞，活塞与筒壁摩擦及活塞重均不计，现将开口端向下竖直缓慢地放入7℃时的水中，筒底恰与水面相平时，筒静止。此时筒内气柱长1.4m，当水温升到27℃时，求筒底露出水面多高？(筒壁厚不计)

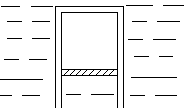
参考答案：
0.1m

本题解析：

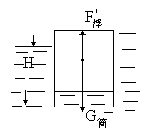
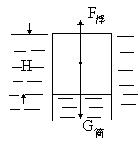
本题难度：简单