1、简答题 如图(a)所示,在电场强度为E、方向水平向右的匀强电场中,有两个质量均为m的小球A、B(可被视为质点),被固定在一根绝缘轻杆的两端,轻杆可绕与电场方向垂直的固定转动轴O无摩擦转动,小球A、B与轴O间的距离分别为l、2l,其中小球B上带有电量为q的正电荷,小球A不带电.将轻杆转动到水平方向后,无初速释放,若已知
=.
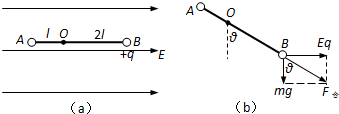
求:(1)轻杆转动到何位置时,小球A、B的速率达到最大.
(2)若l=米,小球A、B的最大速率为多少?
某同学是这样解的:(1)目前轻杆无法平衡,在小球A、B的带动下,开始顺时针转动,当A、B的速度达到最大时,小球B所受的电场力与重力的合力恰与杆平行,如图(b)所示,所以tanθ=qE/mg=…,
(2)对从a图位置到b图位置过程用动能定理求出A、B两球的最大速率.你认为这位同学的解法是否正确,若正确,请完成计算;若不正确,请说明理由,并用你自己的方法算出正确结果.
参考答案:(1)解题方法不正确
因为当小球A、B的速度达到最大时,整个系统处于力矩平衡状态.
当系统处于力矩平衡时:MGA+M电=MGB
设此时轻杆与竖直方向夹角为θ,则
mglsinθ+Eq2lcosθ=2mglsinθ
解得:tanθ=
本题解析:
本题难度:一般
2、填空题 将一根粗细均匀、质量为M的铁丝弯成直角,两直角边边长之比AC:BC=m:n(m>n),C点可绕竖直面转动,如图所示,当直角铁丝静止时,BC边与竖直方向的夹角为θ,则sinθ=______,若在B点悬挂一物体,将使θ=45°,则该物体的质量为______.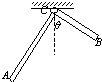
参考答案:
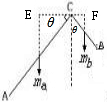
(1)如图,两边的重心分别在中点,质量之比等于长度之比,则
重力之比:Ga:Gb=mag:mbg=ma:mb=m:n,
左边力臂:
La=12AC×cosθ,
右边力臂:
Lb=12BC×sinθ,
由杠杆平衡条件可知:
Ga×La=Gb×Lb,
即:Ga×12AC×cosθ=Gb×12BC×sinθ,
∴sinθ=GaACGbBC×cosθ=m2n2
本题解析:
本题难度:一般
3、实验题 从地面以20 m/s的初速度竖直上抛质量为1 kg的小球,上升的最大高度为16 m,当小球在上升过程中到达某一高度处时,其动能与重力势能恰好相等,此时小球已损失的机械能为________J.(取g="10" m/s2,空气阻力大小恒定)
参考答案:22.2
本题解析:设空气阻力为f,据题设条件有
v02=2×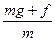 ×h
×h
代入数据解得f="2.5" N
又设在高H处动能和重力势能相等,
mgH= mv2,v2=2gH
mv2,v2=2gH
由运动学公式v02-v2=2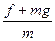 H,H=
H,H=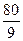 m,
m,
则上升到此高度的过程中损失的机械能为fH="22.2" J.
本题难度:一般
4、简答题 某种汽车的制造标准是车身在横向倾斜300角时不翻倒,如图所示。若车轮间距离为2m,那么车身重心G离斜面的高度应不超过多少米?
参考答案:h = 1.73m。
本题解析:以车为研究对象,进行受力分析

只要重力的作用线不超过车轮的支持面,车就不会翻倒。车轮与斜面的接触点A是支持面的接触边缘。在直角三角形AGO中,∠AGO = 300,AO =  = 1m,则重心高h =
= 1m,则重心高h =  =
=  m = 1.73m。
m = 1.73m。
本题难度:一般
5、填空题 如图,在竖直向下,场强为E的匀强电场中,长为l的绝缘轻杆可绕固定轴O在竖直面内无摩擦转动,两个小球A、B固定于杆的两端,A、B的质量分别为m1和m2(m1<m2),A带负电,电量为q1,B带正电,电量为q2.杆从静止开始由水平位置转到竖直位置,在此过程中电场力做功______,在竖直位置处两球的总动能______.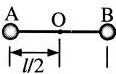
参考答案:因为杆及AB受力的合力矩为顺时针,所以系统沿顺时针转动到竖直位置,电场力对A和B都做正功,电场力对A、B做总功为:
?W=Eq1×l2+Eq2×l2=(q1+q2)El2.
在此过程中重力对A做正功,对B做负功,设两球总动能为Ek,由用动能定理得:
?12(m2-m1)gl+12(q1+q2)El=Ek-0
所以两球总动能为:12[(q1+q2)E+(m2-m1)g]?l
故答案为:(q1+q2)El2,12[(q1+q2)E+(m2-m1)g]?l
本题解析:
本题难度:简单