1、计算题  如图所示，Q为一个原来静止在光滑水平面上的物体，质量为M，它带有一个凹形的不光滑轨道，轨道的ab段是水平的，bc段是半径为R的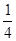圆弧，位于竖直平面内。P是另一个小物体，质量为m，它与轨道间的动摩擦因数为μ。物体P以沿水平方向的初速度v0冲上Q的轨道，已知它恰好能到达轨道顶端c点，后又沿轨道滑下，并最终在a点停止滑动，然后与Q一起在水平面上运动。

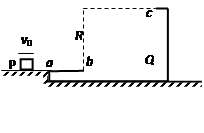
（1）分别求出P从a点滑到c点和从c点滑回a点的过程中各有多少机械能转化为内能？
（2）P位于轨道的哪个位置时，Q的速度达到最大？

参考答案：（1）mgR；（2）θ="arc" tanμ

本题解析：（1）当P在Q上滑行时，水平方向系统受合外力为零，故在水平方向系统动量守恒。当P到达c点时，P和Q具有共同的水平速度V。根据动量守恒定律，
mv0 =" (m+M)" V?（1）
P由a点滑到c点的过程中，系统损失的机械能转化为内能，则根据功能关系
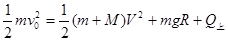?（2）
由（1）、（2）两式得
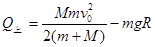? ④
当P到达c点时，P和Q仍具有共同的水平速度V。所以在P由c点滑回到a点的过程中，有?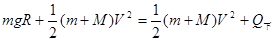
即? Q下=mgR?②
(2)在P从a滑到c的过程中，P对Q的作用力都偏向右侧，因此Q受到向右的作用力，Q将一直加速，到达c点时P、Q间无相互作用；从c滑到b的过程中，P的受力分析示意图如右图所示，其中支持力N偏向左侧，摩擦力f偏向右侧。这个过程的前一阶段，P受到的合外力的水平分力向左，则Q受到合力的水平分力向右，Q将继续加速，当P在水平方向受力平衡的时刻，就是Q速度最大的时刻。? ④
此时满足? f cosθ=" N" sinθ
并且? f = μN
因此得? tanθ=μ
即P所在位置的半径与竖直方向的夹角为? θ="arc" tanμ。? ④

本题难度：一般

2、计算题  某种超导磁悬浮列车是利用超导体的抗磁作用使列车车体向上浮起，同时通过周期性地变换磁极方向而获得推进动力。其推进原理可以简化为如图所示的模型：在水平面上相距b的两根平行直导轨间，有竖直方向等距离分布的方向相反的匀强磁场B1和B2，且B1=B2=B，每个磁场分布区间的长都是a，相间排列，所有这些磁场都以速度v向右匀速平动．这时跨在两导轨间的长为a宽为b的金属框MNQP（悬浮在导轨正上方）在磁场力作用下也将会向右运动．设金属框的总电阻为R，运动中所受到的阻力恒为f，求（1）列车在运动过程中金属框产生的最大电流（2）列车能达到的最大速度（3）在（2）情况下每秒钟磁场提供的总能量

参考答案：（1）列车起动时金属框产生的电流最大，设为
?（2分）
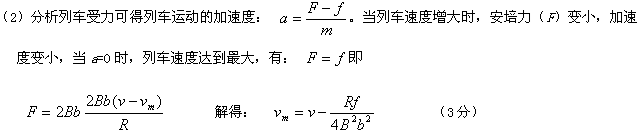（3）由能的转化和守恒，磁场提供的能量一部分转化为电路中的电能进一步转变为回路的焦耳热，另一部分克服阻力f做功，单位时间内有
焦耳热为
最大速度匀速运动时，磁场力等于阻力,?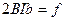
可不阻力做功的功率为
解得

本题解析：略

本题难度：简单

3、选择题  如图所示，带等量异种电荷，质量分别为m1和m2的两个小球A、B，通过绝缘轻弹簧相连接，置于绝缘光滑的水平面上．当突然加一水平向右的匀强电场后，两小球A、B将由静止开始运动，在以后的运动过程中，对两个小球和弹簧组成的系统（设整个过程中不考虑电荷间库仑力的作用且弹簧不超过弹性限度），以下说法正确的是（　　）
A．两个小球所受电场力合力为零，系统机械能守恒
B．电场力对A、B两球均做正功，系统机械能不断增加
C．当弹簧长度达到最大值时，系统动能最大
D．当小球所受电场力与弹簧的弹力相等时，系统动能最大