D.A离开墙面后,弹簧的最大弹性势能为
参考答案:A、根据冲量的定义得从开始到A离开墙面的过程中,墙壁对A有弹力,所以墙对A的冲量不为0,故A错误
B、撤去力F后,B向右运动,弹簧弹力逐渐减小,当弹簧恢复原长时,A开始脱离墙面,这一过程机械能守恒,即满足:
? W=E=12(2m)vB2?
vB=
本题解析:
本题难度:一般
2、选择题 如图所示,一个滑雪运动员从左侧斜坡距离坡底8m处自由滑下,当下滑到距离坡底s1处时,动能和势能相等(以坡底为参考平面);到坡底后运动员又靠惯性冲上斜坡(不计经过坡底时的机械能损失),当上滑到距离坡底s2处时,运动员的动能和势能又相等,上滑的最大距离为4m.关于这个过程,下列说法中正确的是(? )

A.摩擦力对运动员所做的功等于运动员动能的变化
B.重力和摩擦力对运动员所做的总功等于运动员动能的变化
C.s1<4m,s2>2m
D.s1>4m,s2<2m
参考答案:BC
本题解析:根据动能定理合力对对运动员所做的功等于运动员动能的变化.
假设初始重力势能为mgh,那么在距坡底有4m时,重力势能为0.5mgh,但动能小于0.5mgh(因为有摩擦),所以继续下滑,才会出现动能和重力势能相等的时刻,故s1<4m,依次求出s2
解:A、根据动能定理合力对对运动员所做的功等于运动员动能的变化.
这个过程,只有重力和摩擦力对运动员做功,故A错误,B正确.
C、滑雪运动员从左侧斜坡距离坡底8m处自由滑下,当滑到距离坡底4m的时候
此时高度也下落了一半,即:重力势能减少了一半(0.5Ep),还剩下一半(0.5Ep)
由于克服摩擦力做功消耗机械能,所以此时,动能小于重力势能,要再往下滑,才会出现动能等于重力势能的时候.因此,下滑时,当动能等于势能的时候,运动员距离坡底距离小于4m.
到坡底后运动员又靠惯性冲上斜坡,当刚好滑行到距离坡底2m处的时候
此时上升了最大高度的一半,动能也损失了一半0.5Ek (到达最大高度时,剩下的一半也耗尽.)
由于克服摩擦力做功消耗机械能,此时运动员的动能大于重力势能,需要继续往上滑行,才会出现动能等于重力势能的时候.因此,上滑时,动能等于重力势能的时候,运动员距离坡底距离大于2m.故C正确,D错误.
故选BC.
点评:下到坡底的过程中重力势能转化为动能及摩擦力做功产生的热量,上坡中动能转化为重力势能及摩擦力做功产生的热量.抓住能量是守恒的思路解决问题.
本题难度:一般
3、选择题 一个原长为L的轻质弹簧竖直悬挂着。今将一质量为m的物体挂在弹簧的下端,用手托住物体将它缓慢放下,并使物体最终静止在平衡位置。在此过程中,系统的重力势能减少,而弹性势能增加,以下说法正确的是(?)
A.减少的重力势能大于增加的弹性势能
B.减少的重力势能等于增加的弹性势能
C.减少的重力势能小于增加的弹性势能
D.系统的机械能增加
参考答案:A
本题解析:如果由静止自由释放,则系统机械能守恒,在平衡位置小球速度最大,减小的重力势能等于增加的动能和弹性势能之和,所以A对;手的支持力做负功,机械能减小,D错;
本题难度:简单
4、选择题 (文)下列情况中机械能守恒的有
A.作自由落体的物体
B.降落伞在空气阻力作用下匀速下降的过程
C.物体沿光滑斜面下滑的过程
D.物体沿粗糙斜面下滑的过程
参考答案:AC
本题解析:机械能守恒定律的前提条件是只有重力做功,因此作自由落体的物体,机械能守恒,A对。降落伞在空气阻力作用下匀速下降的过程,重力等于阻力,所以有阻力做功,所以B错。物体沿光滑斜面下滑的过程,重力做工外,支持力不做功,所以机械能守恒,C对。物体沿粗糙斜面下滑的过程,有阻力做功,所以机械能不守恒,D错。
点评:本题考查了机械能守恒定律的条件:只有重力做功。在判断机械能守恒定律时可以看看是否有其他外力能量出现,若没有,则机械能守恒。
本题难度:简单
5、计算题 在游乐节目中,选手需借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论。如图所示,他们将选手简化为质量m=60kg的质点,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角α=530,绳的悬挂点O距水面的高度为H=3m,绳长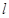 不确定,不考虑空气阻力和绳的质量,浮台露出水面的高度不计。取重力加速度g=10m/s2,sin530=0.8,cos530=0.6。 不确定,不考虑空气阻力和绳的质量,浮台露出水面的高度不计。取重力加速度g=10m/s2,sin530=0.8,cos530=0.6。
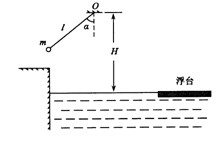
(1)若绳长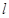 =2m,选手摆到最低点时速度的大小; =2m,选手摆到最低点时速度的大小;
(2)选手摆到最低点时对绳拉力的大小;
(3)若选手摆到最低点时松手,小明认为绳越长,在浮台上的落点距岸边越远;小阳却认为绳越短,落点距岸边越远。请通过推算说明你的观点。
参考答案:(1)4m/s(2)1080N(3)当绳长越接近1.5m时,落点距岸边越远
本题解析:(1)选手摆到最低点过程中机械能守恒,对选手运用机械能守恒定律有:
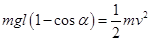 ①? ①?
代入数据得:v=4m/s?
(2)选手过最低点时:
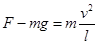 ? ② ? ②
将①式代入②式得:
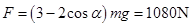 ? ?
由牛顿第三定律可知:选手摆到最低点时对绳拉力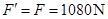 ? ?
(3)选手从最低点开始做平抛运动
水平方向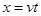 ③? ③?
竖直方向 ④ ④
由①、②、③式得: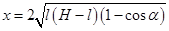 ? ?
当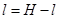 ,即 ,即 时,x有最大值 。 时,x有最大值 。
因此,两人的看法均不正确。当绳长越接近1.5m时,落点距岸边越远。
点评:本题考查到了机械能守恒,圆周运动向心力,平抛运动规律及求极值问题;解答第一问时,由机械能守恒定律计算最低点的速度,答第二问时,一定注意要求的是选手对绳子的拉力,解题过程中是对选手进行受力分析的,故不要忘记应用牛顿第三定律;关于物理当中的极值问题,要会熟练的对式子进行数学分析,从而得出结论。
本题难度:一般
|