1、计算题  在平直公路上，以v1=10m/s匀速行驶的一辆摩托车，与以v2=2m/s的速度行驶的一辆汽车同向行驶，某时刻同时经过A点，以后汽车以a=0.5m/s2的加速度开始加速。求：
（1）经过多少时间汽车追上摩托车？
（2）在汽车追上摩托车之前，两车间的最大距离是多少？

参考答案：解：（1）设经过时间t汽车追上摩托车，此时两车的位移相同，则
由v1t= v2t +1/2at2
得t=32s?
（2）在汽车追上摩托车之前，当两车速度相等时两车间的距离最大，设此时经历的时间为t1，则
由v1= v2+at1
得t1=16s
此时汽车的位移为：X1= v2t1 +1/2at12=96m
摩托车的位移为：X2= v1t1=160m
所以两车间的最大距离为：△X= X2－X1=64m

本题解析：

本题难度：困难

2、计算题  （9分）在平直公路上，甲车在前以υ1 = 12m/s的速度匀速行驶，乙车在后以υ2 = 8m/s的速度匀速行驶。当两车相距L = 24m时，甲车以大小为2m/s2的加速度开始刹车，则甲车刹车后经时间为多长时两车距离最大？并求最大距离sm是多少?

参考答案：28m

本题解析：两车距离最大时乙车的速度与甲车的速度相等，即υ1′ = υ2　　　　?① （1分）
υ1′ = υ1 + at 　　?② （1分）联立①②两式解得：t = 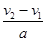?= 2s　?③ （2分）
s2 = υ2t 　　　　?④ （1分）
s1 = 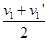t　　?⑤ （1分）
sm =" L" + s1– s2　　?⑥ （1分）
联立④⑤⑥三式，并考虑到③式，解得：sm =" 28m" ⑦ （2分）
点评：在求解本题过程中抓住速度相同是距离最大的临界条件，这是求解本题的突破口

本题难度：简单

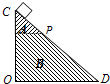
3、选择题  如图所示，等腰直角三角体OCD由不同材料A、B拼接而成，P为两材料在CD边上的交点，且DP＞CP．现OD边水平放置，让小物块从C滑到D；然后将OC边水平放置，再让小物块从D滑到C，小物块两次滑动到达P点的时间相同．下列说法正确的是（　　）
A．A、B材料的动擦因数相同
B．两次滑动中物块到达P点速度大小相等
C．两次滑动中物块到达底端速度大小相等
D．两次滑动中物块到达底端摩擦生热不相等