1、简答题  高空遥感探测卫星在距地球表面高为h处绕地球转动，如果地球质量为M，地球半径为R，人造卫星质量为m，万有引力常量为G，求：
（1）人造卫星的角速度多大？
（2）人造卫星绕地球转动的周期是多少？
（3）人造卫星的向心加速度多大？

参考答案：（1）设卫星的角速度为ω，根据万有引力定律和牛顿第二定律有：
GmM(R+h)2=mω2(R+h)，解得卫星线速度ω=

本题解析：

本题难度：一般

2、填空题  已知地球半径为R，质量为M，自转周期为T，引力常量为G一个质量为m的物体放在赤道处的水平地面上，则物体受到的万有引力F=______，它跟随地球自转需要的向心力为______，它的重力G′=______．

参考答案：根据万有引力定律的计算公式，得物体受到的万有引力：F=GMmR2．
由于知道了周期，所以它跟随地球自转需要的向心力：F向=m(2πT)2R=4π2mRT2
物体放在赤道处的水平地面上随地球一起做圆周运动所需要的向心力由万有引力的一个分力提供的，另一个分力为重力，即F=G′+F向，
所以物体的重力等于万有引力减去向心力，即：G′=F-F向=GMmR2-4π2mRT2．
故答案为：GMmR2，4π2mRT2，GMmR2-4π2mRT2．

本题解析：

本题难度：一般

3、选择题  以下说法正确的是（ ? ）
A．万有引力定律只适用于天体之间的相互作用
B．牛顿测出了引力常量的数值
C．太阳对地球的引力大于地球对太阳的引力
D．万有引力定律把地面上物体运动的规律和天体运动的规律统一了起来

参考答案：D

本题解析：

本题难度：简单

4、选择题  已知质量分布均匀的球壳对内物体的万有引力为零。假设地球是半径为R、质量分布均匀的球体。若地球某处的一矿井深度为d，则矿井底部和地球表面处的重力加速度大小之比为
A．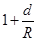
B．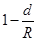
C．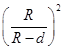
D．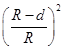

参考答案：B

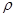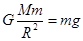本题解析：设地球的密度为，根据，即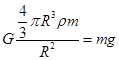，可得地球表面处的重力加速度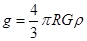，同理矿井深度为d处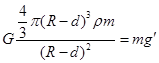，可知，矿井深度为d处重力加速度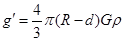，因此矿井底部和地面处的重力加速度大小之比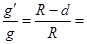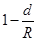，故选B。

本题难度：一般

5、填空题  我国自行研制的“风云一号”、“风云二号”气象卫星运行的轨道是不同的。“一号”是极地圆形轨道卫星。其轨道平面与赤道平面垂直，周期是12h；“二号”是地球同步卫星。两颗卫星相比__________号离地面较高；__________号观察范围较大；__________号运行速度较大。若某天上午8点“风云一号”正好通过某城市的上空，那么下一次它通过该城市上空的时刻将是__________。

参考答案：风云二?、风云一 、?风云一?、 第二天上午8点

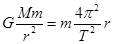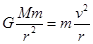本题解析：由得到，“风云二号”周期是24h要大于“风云一号”的周期是12h，所以风云二号离地面较高；二号轨道在赤道的正上方，只能观察赤道周围的范围，一号的轨道绕两极运动，由于地球自传，即观察的范围较大；由得到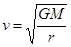，一号的半径小，一号运行速度大；根据周期关系，地球自传一周，一号卫星转两周，所以应是满足地球自传的一个周期，一号卫星第二次经过该点，即第二天上午8点。

本题难度：简单