1、选择题  一飞船绕地球做匀速园周运动，飞船离地面的高度为h，其内有一质量为m的人站在可称体重的台秤上，用R表示地球半径，g表示地球表面的重力加速度，g，表示飞船所在处的地球引力加速度，FN表示人对台秤的压力，则下列判断正确的是（　　）
A．g，=0
B．g，=

参考答案：A、忽略地球自转的影响，根据万有引力等于重力列出等式
在地球表面：GMmR2=mg
在离地面的高度为h处：GMm(R+h)2=mg，
解得：g=R2(R+h)2g，故A错误，B正确．
C、在绕地球做匀速园周运动的飞船内，各个物体处于完全失重的状态．
各个物体的重力完全提供向心力．
所以人站在可称体重的台秤上，人与台秤无弹力，所以FN=0，故C正确，D错误．
故选BC．

本题解析：

本题难度：一般

2、选择题  经长期观测人们在宇宙中已经发现了“双星系统”，“双星系统”由两颗相距较近的恒星组成，每个恒星的直径远小于两个星体之间的距离，而且双星系统一般远离其他天体。如图所示，两颗星球组成的双星，在相互之间的万有引力作用下，绕连线上的O点做周期相同的匀速圆周运动。现测得两颗星之间的距离为L，质量之比为m1：m2＝3：2。则可知（?）

A．m1：m2做圆周运动的角速度之比为2：3
B．m1：m2做圆周运动的线速度之比为3：2
C．m1做圆周运动的半径为
D．m2做圆周运动的半径为

参考答案：C

本题解析：由于双星的周期相同，故它们的角速度也相同，A不对；又由于两星受到的万有引力是相等的，根据牛顿第二定律得，加速度度之比a1：a2=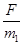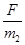：=m2：m1=2：3，由圆周运动的规律可得a=ωv，故m1：m2做圆周运动的线速度之比也为2：3，B是不对的；再由v=ωr可得，m1：m2做圆周运动的半径之比也为r1：r2=2：3，又因为r1+r2=L，故r1=，r2=，C是正确的，D不对。

本题难度：一般

3、选择题  我国未来将建立月球基地，并在绕月轨道上建造空间站。如图所示，关闭动力的航天飞机在月球引力作用下向月球靠近，并将与空间站在B处对接，已知空间站绕月轨道半径为r，周期为T，万有引力常量为G，下列说法中正确的是

[? ]
A．图中航天飞机正加速飞向B处
B．航天飞机在B处由椭圆轨道进入空间站轨道必须点火减速
C．根据题中条件可以算出月球质量
D．根据题中条件可以算出空间站受到月球引力的大小

参考答案：ABC

本题解析：

本题难度：一般

4、选择题  如图所示，a、b两颗质量不相同的人造卫星，在不同的圆形轨道上绕地球做匀速圆周运动，下列说法中正确的是

A．a的线速度一定大于b的线速度
B．a的加速度一定大于b的加速度
C．a的周期一定大于b的周期
D．a的向心力一定大于b的向心力

参考答案：AB

本题解析：
A、根据万有引力提供向心力，有：

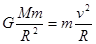
解得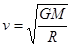，轨道半径越大，速度越小，故A正确；
B、根据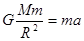，解得a=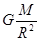，故半径越小，加速度越大，故B正确；
C、周期T=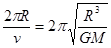，故轨道半径越小，周期越小，故C错误；
D、向心力F=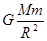，两颗卫星质量本不同，故无法比较向心力，故D错误；
故选AB。

本题难度：简单

5、计算题  天文学家将相距较近、仅在彼此间引力作用下运行的两颗恒星称为双星。双星系统在银河系中很普遍。利用双星系统中两颗恒星的运动特征可推算出它们的总质量。已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动，周期均为T，两颗恒星之间的距离为r，试推算这个双星系统的总质量。（引力常量为G）

参考答案：解：设两颗恒星的质量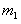分别为、，做圆周运动的半径分别为、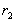，角速度分别为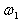、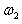。根据题意有
==，+=
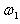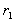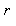
根据万有引力定律和牛顿运动定律，有
，
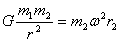
联立以上各式解得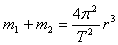

本题解析：

本题难度：一般