1、简答题 (1)用如图1实验装置验证m1、m2组成的系统机械能守恒.m2从高处由静止开始下落,m1上拖着的纸带打出一系列的点,对纸带上的点迹进行测量,即可验证机械能守恒定律.下图给出的是实验中获取的一条纸带:0是打下的第一个点,每相邻两计数点间还有4个点(图中未标出),计数点间的距离如图2所示.已知m1=50g、m2=150g,则(g取10m/s2,结果保留两位有效数字)
①在纸带上打下记数点5时的速度v=______m/s;
②在打点0~5过程中系统动能的增量△EK=______J,系统势能的减少量△EP=______J,由此得出的结论是______;
③若某同学作出
v2-h图象如图3,则当地的实际重力加速度g=______m/s2.
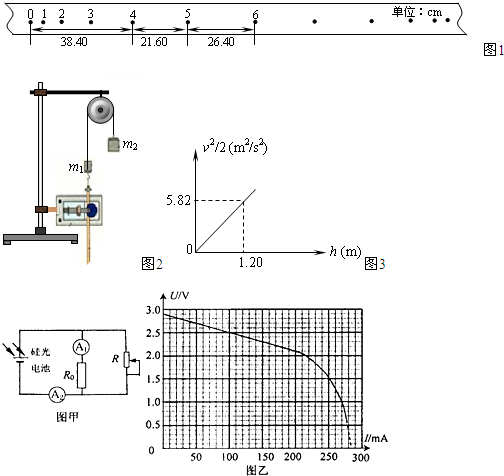
(2)某同学为了测定某硅光电池的电动势和内电阻,设计了如图甲所示电路.图中与理想电表A1串联的定值电阻的阻值为R0,在一定强度的光照下进行下述实验(计算结果小数点后保留两位数字):
①闭合开关,调节滑动变阻器,读出电流表A1、A2的值I1、I2.为了作出此电池的U-I曲线,需要计算出电路的路端电压U,则U=______(用题中所给字母表示);
②根据测量数据作出该硅光电池的U-I图象如图乙所示,该电池的电动势E=______V,在流过电流表A2的电流小于200mA的情况下,此电池的内阻r=______Ω;
③若将该硅光电池两端接上阻值为6Ω的电阻,此时对应的电池内阻r=______Ω.
参考答案:(1)①根据在匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度,可知打第5个点时的速度为:
v5=x46t46=2.4m/s
②物体的初速度为零,所以动能的增加量为
△EK=Ek5-0=12(m1+m2)v52=0.58 J.
重力势能的减小量等于物体重力做功,故:△EP=W=mgh=0.60J;
由此可知动能的增加量和势能的减小量基本相等,因此在在误差允许的范围内,m1、m2组成的系统机械能守恒.
故答案为:0.58,0.60,在误差允许的范围内,m1、m2组成的系统机械能守恒.
③由于△EK=Ek5-0=12(m1+m2)v52=△Ep=(m2-m1)gh
由于(m1+m2)=2(m2-m1)
所以得到:12v2=g2h
所以12v2-h图象的斜率k=g2
g=9.7m/s2.
(2)①理想电流表和定值电阻构成一电压表,可测量外电压.所以U=I1R0.
?②在硅光电池的U-I图象,当I=0,U=E,图线斜率的绝对值表示内阻.所以E=2.90V,在流过电流表A2的电流小于200mA的情况下,此电池的内阻r=4.00Ω.
?③作出6Ω定值电阻的U-I图线,是一条过原点的直线,该直线与图乙中电源的外电压和电流图线有交点,交点对应的电压、电流表示硅光电池两端接上阻值为6Ω的电阻时的电压和电流.所以r=E-UI=5.60.
故答案为:(1)①2.4?②0.58;0.60;在误差允许的范围内,m1、m2组成的系统机械能守恒;③9.7
(2)I1R0;?(2)2.90;?4.00?(3)5.60
本题解析:
本题难度:一般
2、计算题 如图所示,一束带负电荷e,质量为m的电子流,平行于x轴以速度v0射入第Ⅰ象限区域,为使这束电子能经过x轴上的b点,可在第Ⅰ象限某区域加一个正y方向的匀强电场,场强大小为E,其范围沿y方向无限大,沿x轴方向宽度为s,已知oa=L,ob=2s。求电场右边界线跟b点的距离。
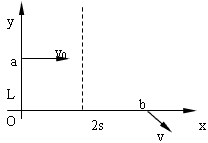
参考答案:解:电子在电场中的轨迹是一条抛物线,而且一定经过b点,要考虑b点可能在电场中,也可能在电场外,所以会出现几种可能的情况,电子在电场中沿-y方向的偏移量总可以用下式表示:
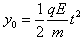 ?①
?①
第一种情况:如果恰好y0=L,则电场的右边界恰好经过b点,左边界在ob的中点,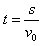
将①式的y0以L代入,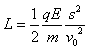
第二种情况:如果b点在电场内,电场右边界跑到b点的右方,则s>x,L<y0,t=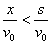
因为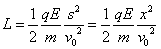
所以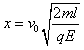
结论:电场的左边界位于b点左方x处,右边界距b点为向右(s-x)处
第三种情况:整个电场都在b的左方
一定有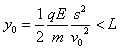
注意到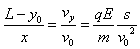
可求得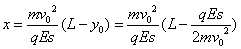
可见电场的右边界在b点左方x远处
本题解析:
本题难度:困难
3、简答题 某仪器用电场和磁场来控制电子在材料表面上方的运动.如图所示,材料表面上方矩形区域PP"N"N充满竖直向下的匀强电场,宽为d;矩形区域NN′M′M充满垂直纸面向里的匀强磁场,磁感应强度为B,长为3s,宽为s;NN"为磁场与电场之间的薄隔离层.一个电荷量为e、质量为m、初速为零的电子,从P点开始被电场加速经隔离层垂直进入磁场,电子每次穿越隔离层,运动方向不变,其动能损失是每次穿越前动能的10%,最后电子仅能从磁场边界M"N"飞出.不计电子所受重力.
(1)求电子第二次与第一次圆周运动半径之比;
(2)求电场强度的取值范围;
(3)A是M′N′的中点,若要使电子在A、M′间垂直于AM′飞出,求电子在磁场区域中运动的时间.
参考答案:
(1)设圆周运动的半径分别为R1、R2、…Rn、Rn+1…,第一和第二次圆周运动速率分别为v1和v2,
动能分别为Ek1和Ek2
由:Ek2=0.81Ek1
R1=mv1Be,R2=mv2Be
Ek1=12mv12,Ek2=12mv22
得:R2:R1=0.9:1
(2)设电场强度为E,第一次到达隔离层前的速率为v′,根据能量关系有:
eEd=12mv′2
0.9×12mv′2=12mv21
R1≤s
得:E≤5B2es29md
又由:Rn=0.9n-1R1
2R1(1+0.9+0.92+…+0.9n+…)=3s
得:E>B2es280md
电场强度的取值范围为B2es280md<E≤5B2es29md
(3)设电子在匀强磁场中,圆周运动的周期为,运动的半圆周个数为n,运动总时间为t
由题意,有:
2R1(1-0.9n)1-0.9+Rn+1=3s
R1≤s
Rn+1=0.9nR1
Rn+1≥s2
得:n=2
由题意知,电子在磁场中做了2个半圆和一个14圆,
由:T=2πmeB
得:t=2×12T+14T=5πm2eB
答:(1)电子第二次与第一次圆周运动半径之比是0.9:1.
(2)电场强度的取值范围是B2es280md<E≤5B2es29md
(3)电子在磁场区域中运动的时间是5πm2eB
本题解析:
本题难度:一般
4、简答题 如图所示的装置,在加速电场U1内放置一根塑料管AB(AB由特殊绝缘材料制成,不会影响电场的分布),紧靠其右侧的是两块彼此平行的水平金属板,板长为L,两板间距离为d.一个带负电荷的小球,恰好能沿光滑管壁运动.小球由静止开始加速,离开B端后沿金属板中心线水平射入两板中,若给两水平金属板加一电压U2,当上板为正时,小球恰好能沿两板中心线射出;当下板为正时,小球射到下板上距板的左端
处,求:
(1)U1:U2;
(2)若始终保持上板带正电,为使经U1加速的小球,沿中心线射入两金属板后能够从两板之间射出,两水平金属板所加电压U的范围是多少?(请用U2表示)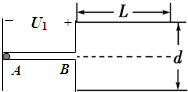
参考答案:(1)设粒子被加速后的速度为v0,当两板间加上电压U2
如上板为正时,U2qd=mg,U2=mgdq
如下板为正时,a=mg+U2qdm=2g
12d=12?2g(L4v0)2
qU1=12mv02.
解得U1U2=L216d2
(2)当上板加最大电压Um时,粒子斜向上偏转刚好穿出:
t=Lv0
Umqd-mg=ma1
d2=12a1t2
得Um=98U2
若上板加上最小正电压Un时,粒子向下偏转恰穿出:mg-Unqd=ma2
d2=12a2t2
得Un=78U2
电压的范围为:78U2<U<98U2
答:(1)U1:U2=L216d2.
(2)两水平金属板所加电压U的范围是78U2<U<98U2.
本题解析:
本题难度:一般
5、选择题 图甲是某同学设计的电容式速度传感器的原理图,在两极板间电压恒定的条件下,极板上所带电荷量Q将随待测物体的上下运动而变化,若Q随时间t的变化关系为Q= (a、b为大于零的常数)。其图象如图乙所示,那么图丙、图丁中反映极板间场强大小E和物体速率v随时间t变化的图象可能是
(a、b为大于零的常数)。其图象如图乙所示,那么图丙、图丁中反映极板间场强大小E和物体速率v随时间t变化的图象可能是

[? ]
A.①和③
B.①和④
C.②和③
D.②和④
参考答案:C
本题解析:
本题难度:一般