1、简答题 如图所示,在竖直向下的匀强电场中有一绝缘的光滑离心轨道,一个带负电的小球从斜轨道上的A点由静止释放,沿轨道滑下,已知小球的质量为m,电量大小为-q,匀强电场的场强大小为E,斜轨道的倾角为α (小球的重力大于所受的电场力) 。
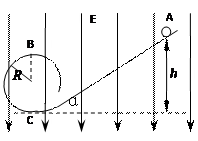
(1)求小球沿斜轨道下滑的加速度的大小;
(2)若使小球通过半径为R的圆轨道顶端的B点时不落下来,求A点距水平地面的高度h至少应为多大?
(3)若小球从斜轨道h =" 5R" 处由静止释放,假设能够通过B点,求在此过程中小球机械能的改变量。
?
参考答案:(1)(mg-qE ) 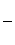
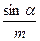 ?(2)h =
?(2)h = ?(3)-3REq?
?(3)-3REq?
本题解析:
(1)?据牛顿第二定律:
(mg-qE)Sinα= ma ?…………………… (2分)
a = (mg-qE ) 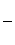
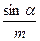 ?…………………… (2分)
?…………………… (2分)
(2)若小球刚好在B点不下落,据牛顿第二定律?
mg-qE =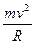 ?①?…………………… (3分)
?①?…………………… (3分)
小球由A到B,据动能定理mv2/2
(mg-qE)(h-2R) = 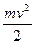
 ?②?…………………… (3分)
?②?…………………… (3分)
①②式联立,得 h = ?…………………… (2分)
?…………………… (2分)
(3)小球从静止开始沿圆弧轨道运动到B点的过程中,机械能的变化量为△E电
由?△E机= W电?…………………… (3分)
? W电=-3REq
?得△E机=-3REq?…………………… (3分)
?用△E机=EB - EA方法解答同样得分
本题难度:一般
2、计算题 如图,在 平面第一象限整个区域分布匀强电场,电场方向平行
平面第一象限整个区域分布匀强电场,电场方向平行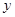 轴向下,在第四象限内存在有界匀强磁场,左边界为
轴向下,在第四象限内存在有界匀强磁场,左边界为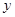 轴,右边界为
轴,右边界为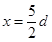 的直线,磁场方向垂直纸面向外。质量为
的直线,磁场方向垂直纸面向外。质量为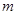 、带电量为
、带电量为 的粒子从
的粒子从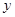 轴上
轴上 点以初速度
点以初速度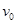 垂直
垂直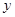 轴射入匀强电场,在电场力作用下从
轴射入匀强电场,在电场力作用下从 轴上
轴上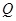 点以与
点以与 轴正方向成45°角进入匀强磁场。已知
轴正方向成45°角进入匀强磁场。已知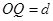 ,不计粒子重力。求:
,不计粒子重力。求:
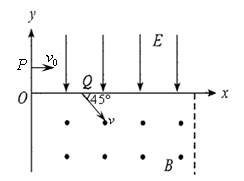
(1) 点坐标;
点坐标;
(2)要使粒子能再进入电场,磁感应强度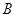 的取值范围;
的取值范围;
(3)要使粒子能第二次进入磁场,磁感应强度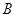 的取值范围。
的取值范围。
参考答案:(1)(0,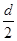 )(2)
)(2)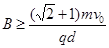 (3)
(3)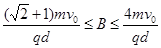
本题解析:(1)设粒子进入电场时y方向的速度为vy ?,则 ?
?
设粒子在电场中运动时间为t,则
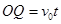 ?
?
 ?
?
由以上各式,解得
 点坐标为(0,
点坐标为(0,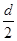 )?
)?
(2)粒子刚好能再进入电场的轨迹如图所示,设此时的轨迹半径为r1,则
 ?
?
解得: ?
?
令粒子在磁场中的速度为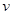 ?,则
?,则 ?
?
根据牛顿第二定律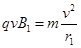
解得: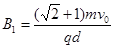 ?
?
要使粒子能再进入电场,磁感应强度B的范围?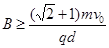 ?
?
(3)要使粒子刚好从 处第二次进入磁场的轨迹如图,
处第二次进入磁场的轨迹如图,
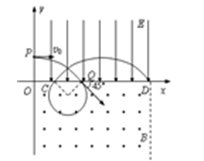
粒子从P到Q的时间为t,则粒子从C到D的时间为2t,所以? ?
?
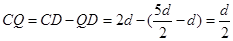 ?
?
设此时粒子在磁场中的轨道半径为r2,
由几何关系?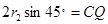 ?
?
解得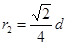 ?
?
根据牛顿第二定律 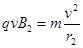 ?
?
解得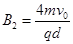 ?
?
要使粒子能第二次进磁场,粒子必须先进入电场,故磁感应强度B要满足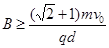 ?
?
综上所述要使粒子能第二次进磁场,磁感应强度B要满足
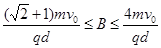
本题难度:一般
3、选择题 闭合回路由电阻R与导线组成,其内部磁场大小按B-t图变化,方向如图,则回路中
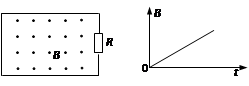
A.电流方向为顺时针方向
B.磁通量的变化率恒定不变
C.电流强度越来越大
D.产生的感应电动势越来越大
参考答案:AB
本题解析:考点:
专题:计算题.
分析:由B-t图象可知磁感应强度的变化情况,则由磁通量的定义可知磁通量的变化率;再由楞次定律可判断电流方向;由法拉第电磁感应定律可求得感应电动势.
解答:解:由图象可知,磁感应随时间均匀增大,则由?=BS可知,磁通量随时间均匀增加,故其变化率恒定不变,故B正确;
由楞次定律可知,电流方向为顺时针,故A正确;
由法拉第电磁感应定律可知,E=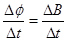 S,故感应电动势保持不变,电流强度不变,故CD均错;
S,故感应电动势保持不变,电流强度不变,故CD均错;
故选AB.
点评:本题考查楞次定律及法拉第电磁感应定律的应用,二者分别判断感应电流的方向和大小,应熟练掌握.
本题难度:简单
4、计算题 如图所示,在半径为R的绝缘圆筒内有匀强磁场,方向垂直于纸面向里,圆筒正下方有小孔C与平行金属板M、N相通。两板间距离为d,两板与电动势为E的电源连接。一电荷量为-q、质量为m的带电粒子(重力忽略不计),开始时静止于C点正下方紧靠N板的A点,经电场加速后从C点进入磁场,并以最短的时间从C 点射出。已知带电粒子与筒壁的碰撞无电荷量的损失,且碰撞后以原速率返回,求:
(1)筒内磁场的磁感应强度大小;
(2)带电粒子从A点出发至第一次回到A点所经历的时间。
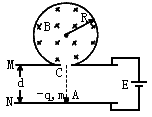
参考答案:解:(1)如图所示,带电粒子从C孔进入,与筒壁碰撞两次再从C孔射出经历的时间最短,设粒子在磁场中做匀速圆周运动的速率为v,有: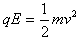
得:v=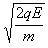
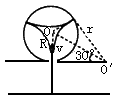
由几何关系可知,粒子在磁场中的运动半径为:r=Rcot30°
粒子在磁场中运动时有:qvB=
解得:B=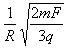
(2)粒子从A到C运动时的加速度为: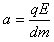
由d= 得,粒子从A到C的时间为:t1=
得,粒子从A到C的时间为:t1=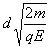
粒子在磁场中运动的时间为: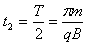
解得:t2=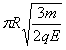
因此带电粒子从A点出发至第一次回到A点的时间为:t=2t1+t2=(2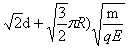
本题解析:
本题难度:困难
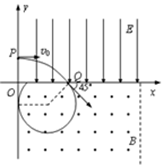
5、计算题 (15分)如图所示,直线OA与x轴成135°角,x轴上下方分别有水平向右的匀强电场E1和竖直向上的匀强电场E2,且电场强度E1=E2=10N/C,x轴下方还存在垂直于纸面向外的匀强磁场B,磁感应强度B=10T。现有一质量m=1.0×10-5kg,电荷量q=1.0×10-5C的带正电尘粒在OA直线上的A点静止释放,A点离原点O的距离d=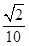 m(g取10m/s2,).求:
m(g取10m/s2,).求:
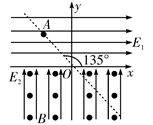
(1)尘粒刚进入磁场区域时的速度v的大小;
(2)从进入磁场区域开始到离开磁场区域所经历的时间t;
(3)第一次回到OA直线上的某位置离原点O的距离L。
参考答案:(1)2m/s(2)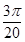 s(3)0.13m
s(3)0.13m
本题解析:(1)F=Eq=1×10-4N?, 1分?
尘粒在电场E中受到的合外力为
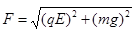 ?,1分?
?,1分?
合外力F和水平方向间的夹角φ为tanφ=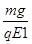 =1
=1
φ=45°?
尘粒在电场E1中的加速度a大小为a=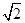 g , 2分
g , 2分
v=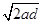 =2m/s?,2分?
=2m/s?,2分?
(2)进入磁场后尘粒在磁场中转动的周期T和转动半径R分别为
T=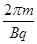 =
=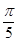 s,2分
s,2分
R= =0.2m? 2分
=0.2m? 2分
轨迹如图所示,由图可知,t=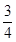 T=
T=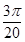 s? 2分
s? 2分
(3)出磁场后尘粒在电场E1中做类平抛运动
OC=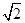 R=
R=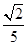
t1=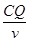 =
=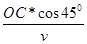 =
=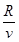 =0.1s? 2分
=0.1s? 2分
B位置离原点O的距离L大小为
L=OC·sin45-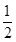 at1=R-
at1=R-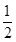 at1=0.13m? 2 分
at1=0.13m? 2 分
点评:电荷在匀强磁场中做匀速圆周运动,关键是画出轨迹,由几何知识求出半径.定圆心角,求时间.
本题难度:一般