1、简答题 如图所示,在竖直向下的匀强电场中有一绝缘的光滑离心轨道,一个带负电的小球从斜轨道上的A点由静止释放,沿轨道滑下,已知小球的质量为m,电量大小为-q,匀强电场的场强大小为E,斜轨道的倾角为α (小球的重力大于所受的电场力) 。
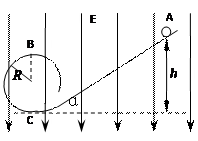
(1)求小球沿斜轨道下滑的加速度的大小;
(2)若使小球通过半径为R的圆轨道顶端的B点时不落下来,求A点距水平地面的高度h至少应为多大?
(3)若小球从斜轨道h =" 5R" 处由静止释放,假设能够通过B点,求在此过程中小球机械能的改变量。
?
2、计算题 如图,在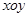 平面第一象限整个区域分布匀强电场,电场方向平行
平面第一象限整个区域分布匀强电场,电场方向平行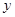 轴向下,在第四象限内存在有界匀强磁场,左边界为
轴向下,在第四象限内存在有界匀强磁场,左边界为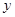 轴,右边界为
轴,右边界为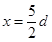 的直线,磁场方向垂直纸面向外。质量为
的直线,磁场方向垂直纸面向外。质量为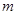 、带电量为
、带电量为 的粒子从
的粒子从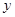 轴上
轴上 点以初速度
点以初速度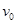 垂直
垂直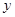 轴射入匀强电场,在电场力作用下从
轴射入匀强电场,在电场力作用下从 轴上
轴上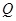 点以与
点以与 轴正方向成45°角进入匀强磁场。已知
轴正方向成45°角进入匀强磁场。已知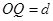 ,不计粒子重力。求:
,不计粒子重力。求:
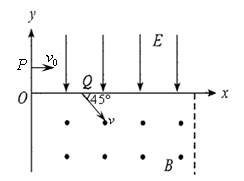
(1) 点坐标;
点坐标;
(2)要使粒子能再进入电场,磁感应强度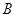 的取值范围;
的取值范围;
(3)要使粒子能第二次进入磁场,磁感应强度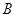 的取值范围。
的取值范围。
3、选择题 闭合回路由电阻R与导线组成,其内部磁场大小按B-t图变化,方向如图,则回路中
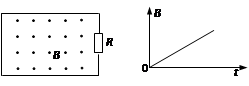
A.电流方向为顺时针方向
B.磁通量的变化率恒定不变
C.电流强度越来越大
D.产生的感应电动势越来越大
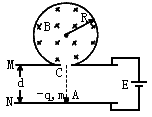
4、计算题 如图所示,在半径为R的绝缘圆筒内有匀强磁场,方向垂直于纸面向里,圆筒正下方有小孔C与平行金属板M、N相通。两板间距离为d,两板与电动势为E的电源连接。一电荷量为-q、质量为m的带电粒子(重力忽略不计),开始时静止于C点正下方紧靠N板的A点,经电场加速后从C点进入磁场,并以最短的时间从C 点射出。已知带电粒子与筒壁的碰撞无电荷量的损失,且碰撞后以原速率返回,求:
(1)筒内磁场的磁感应强度大小;
(2)带电粒子从A点出发至第一次回到A点所经历的时间。
5、计算题 (15分)如图所示,直线OA与x轴成135°角,x轴上下方分别有水平向右的匀强电场E1和竖直向上的匀强电场E2,且电场强度E1=E2=10N/C,x轴下方还存在垂直于纸面向外的匀强磁场B,磁感应强度B=10T。现有一质量m=1.0×10-5kg,电荷量q=1.0×10-5C的带正电尘粒在OA直线上的A点静止释放,A点离原点O的距离d=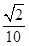 m(g取10m/s2,).求:
m(g取10m/s2,).求:
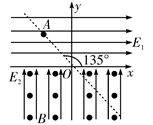
(1)尘粒刚进入磁场区域时的速度v的大小;
(2)从进入磁场区域开始到离开磁场区域所经历的时间t;
(3)第一次回到OA直线上的某位置离原点O的距离L。